Leitfaden
This post is also available in:
 English (Englisch)
English (Englisch)
Zur Konkretisierung einer Aussage nutzt Musik aus der Wortsprache vertraute Techniken wie Betonung, Rhythmisierung, Modulationen der Lautstärke und der Tonhöhe. Ihr eigen ist die Ausprägung von Tonordnungssystemen. Als besonders wirkmächtig erwies sich die Legierung von melodischen und harmonischen Ordnungskriterien. Im europäischen Kulturraum gipfelte die diesbezügliche Entwicklung in der Dur-Moll-Tonalität und begünstigte die analytische Privilegierung der Harmonik. Um diese zu erschließen, wurden mit der Stufen- sowie der Funktionstheorie zwei empirisch basierte Modelle entwickelt. Deren Regeln prägten fortan die Auseinandersetzung mit tonalen Entwicklungen.
Das Primat der Dur-Moll-Tonalität samt der aus ihr abgeleiteten Theoriebildung beschränkte eine Auseinandersetzung mit tonalen Prozessen in den Randbereichen oder jenseits der Grenzen dieses Systems. Die harmonisch-tonalen Innovationen besonders ab Beginn des 19. Jahrhunderts liessen sich daher nicht mehr angemessen erfassen; außerhalb des Systems zu konstatierende tonale Prozesse ohnehin nicht. Arnold Schönberg forderte in seiner Harmonielehre folgerichtig ein Zurückfragen von den Regeln des Dur-Moll-Systems hin zu den grundlegenden Gesetzmäßigkeiten des Phänomens Tonalität. Angesichts der Dynamik und Vielfältigkeit der abendländischen Musikentwicklung hatte sich die Musikwissenschaft freilich von der Erörterung von Grundsatzfragen längst entfernt und sich auf die Entwicklung analytischer Verfahren in der Auseinandersetzung mit konkret vorgefundenen Kompositionen konzentriert. Der Aufstieg des Fachs ab dem 18. Jahrhundert verdankt sich wesentlich dieser Arbeit am Werk. Schönbergs vermeintlich in eine überwundene Vergangenheit zurückweisendes Postulat einer systemübergreifend abstrakten Gesetzmäßigkeit blieb daher ohne nennenswerte Resonanz.
Es war Schönberg selbst, der schließlich eine versteckte Symmetrie als grundlegend für tonal-harmonische Prozesse identifizierte, diese als Rückgrat seiner komplementären Reihen verwendete und die immanente tonale Option bei Bedarf tatsächlich aktivierte. Er dokumentierte sein Wissen anhand seiner in den Jahren 1921-1923 entstandenen Suite für Klavier op. 25. Deren Reihe ist einerseits komplementär und somit konform zur grundlegenden Tonalitätssymmetrie. Zugleich lässt sie sich in drei Segmente unterteilen, die symmetrisch zu jener Achse sind, welche im Terzentorus senkrecht auf der für harmonische Tonalität konstitutiven Symmetrieachse steht. Das letzte dieser Segmente ist der Krebs der prominenten Tonfolge BACH. Im Jahr 1921 gestattete sich Schönberg gegenüber seinem Schüler Josef Rufer eine Andeutung: „Ich habe eine Entdeckung gemacht, durch welche die Vorherrschaft der deutschen Musik für die nächsten hundert Jahre gesichert ist.“ Da eine Entdeckung etwas bereits Vorhandenes, aber bisher nicht Bekanntes bezeichnet, zielte er offenbar auf einen über die Entwicklung der Zwölftontechnik hinausgehenden, mit dieser jedoch aufgrund der zeitlichen Koinzidenz in einem Zusammenhang stehenden Sachverhalt von großer Tragweite. Tatsächlich ergibt sich aus der Übertragung der Tonalitätssymmetrie von der Dur-Moll-Tonalität auf die eigene, fortan komplementäre Reihentechnik die faszinierende Perspektive einer Suspendierung der Dreiklangsästhetik ohne Preisgabe der Tonalität.
Während die Technik des Komponierens mit komplementären Reihen nicht zuletzt von Schönbergs Schülern Alban Berg und Anton Webern übernommen wurde, findet sich kein Hinweis, dass seitens ihres Erfinders eine Aufklärung über die tonale Implikation der zugrundeliegenden Symmetrie stattgefunden hätte. Schönberg belässt es bei allgemein gehaltenen Anmerkungen zur Tonalität einer Zwölftonreihe und bei Kritik an der Qualität der bald einsetzenden Reihenanalysen. Infolge dieser Zurückhaltung blieb die Möglichkeit ungenutzt, die empirisch gegründete Analyse harmonischer Prozesse bereits in den 1920er Jahren auf eine solidere Grundlage zu stellen. Diesbezügliche Forderungen aus Schönbergs umfangreicher Harmonielehre mündeten nicht in die Entwicklung adäquater analytischer Verfahren. Eine verbindlichere Erschließung der tonalen Orientierung beispielsweise in den Werken der Romantik, des Impressionismus und partiell der Dodekaphonie blieb zunächst außer Reichweite. Eingreifende Folgen hatte Schönbergs Verschwiegenheit für die Auseinandersetzung mit seinem Œuvre sowie dessen kompositionsgeschichtlicher Wirkung. In der Literatur wird die strukturbildende Funktion komplementärer Reihen in atonalen Kompositionen durchweg ohne Kenntnis der immanenten tonalen Option gewürdigt. Tatsächlich hat Schönberg diese bei Bedarf ins Werk gesetzt, wobei stets die jeweilige Aussageintention durch die Übereinstimmung mit dem formalen Verlauf verstärkt wird.
Die Existenz der Tonalitätssymmetrie K wurde im Jahr 2003 erstmals dokumentiert. Es folgte 2007 der Nachweis, dass nicht nur komplementäre Reihen, sondern auch die klassische Kadenzharmonik bis ins Detail aus dieser Symmetrie abgeleitet werden können. 2013 wurde ein aus K abgeleitetes analytisches Verfahren – die ci-Analyse – vorgestellt, mit dessen Hilfe sich tonale Prozesse in Kompositionen der Romantik des Impressionismus und der Dodekaphonie Schönbergs detailliert nachweisen lassen. Die Auseinandersetzung mit K und die Integration der Erkenntnisse in den wissenschaftlichen Diskurs erwies sich jedoch als langwieriger Prozess. Das liegt zu einem nicht geringen Teil an der Abstraktheit und Neuartigkeit des Gegenstands. In einem empirisch geprägten Fach wie der Musikwissenschaft müssen entsprechende Grundlagen erst erarbeitet werden. Eine weitere Hürde ergibt sich daraus, dass die durch die Arbeit mit der Symmetrie K erzielten Ergebnisse in Gegensatz zu Lehrmeinungen stehen, welche sich im Lauf der Jahrzehnte zu vermeintlichen Gewissheiten verfestigt haben, und auch den kompositionsgeschichtlichen Diskurs dominieren. Dass das vermeintlich vom Zerfall der tonalen Strukturen geprägte 19. Jahrhundert Strategien zur subtileren Steuerung des tonalen Verlaufs entwickelte erscheint ebenso gewöhnungsbedürftig wie das Ansinnen, Schönberg nicht einseitig als Vater der Atonalität zu rezipieren sondern zugleich seine Leistung zu würdigen, die tonalen Errungenschaften des 19. Jahrhunderts in die Entwicklung eines neuen Tonordnungssystems zu integrieren.
Eine weitere Hürde gründet in der zeitaufwendigen Umständlichkeit der ci-Analyse per Hand. Das Herauslesen und tabellarische Erfassen von Komplementärintervallen ist eine Geduldsprobe und verzeiht keine Flüchtigkeiten. Die Entwicklung einer App, welche diesen Vorgang in weiten Teilen automatisiert, hat hier Abhilfe geschaffen. Anliegen der ci-Homepage und des vorliegenden Leitfadens ist hieran anknüpfend, den Zugang zu dieser neuen Analysemethode weiter zu vereinfachen, und eine anwendungsorientierte Vermittlung analytischer Kompetenz zu erleichtern. Ein wichtiger Schritt ist dabei die Emanzipierung von den Einschränkungen gewohnter Perspektiven, die Gewinnung eines neuen Standpunkts. Sodann zeigt eine detaillierte Anleitung, wie man mit Hilfe der App ein Werk harmonisch-tonal durchanalysiert und die automatisch in Tabellen dokumentierten Ergebnisse interpretieren kann. Beispielanalysen zeigen sodann, welche erweiterten Einsichten sich aus der Anwendung des Verfahrens abhängig von der jeweiligen Epoche ergeben. Während sich im Hinblick auf klassische Konzepte ein vertieftes Verständnis der bekannten Regeln ergibt, führt die Analyse vor allem romantischer, impressionistischer und dodekaphoner Kompositionen Schönbergs zu detaillierten neuen Erkenntnissen. An die Stelle der Beschreibung einer harmonischen Situation als beispielsweise vage oder gar atonal tritt nunmehr die genaue Benennung der infolge einer harmonischen Progression vorhandenen tonalen Optionen. Während eine Eliminierung tonaler Perspektive bisher in gleicher Weise als freitonal oder atonal bezeichnet wurde wie eine sehr weitgehende Offenheit, erfasst ci-Analyse derartige Konstellationen als gegensätzlich und ermöglicht damit eine Präzisierung der möglichen inhaltlichen Intention respektive Aussage.
Die Dur-Moll-Tonalität, deren Weiterungen im 19. Jahrhundert sowie die Zwölftontechnik Arnold Schönbergs sind aus der versteckten Symmetrie K ableitbar. Durch die Auswertung der durch K generierten Komplementärintervalle lassen sich daher erstmals tonale Prozesse über die Grenzen verschiedener Tonsysteme hinweg detailliert erfassen und tonale Randbereiche der Analyse zugänglich machen. Dank einer speziell entwickelten Analyse-App ist das Verfahren für jeden Interessierten anwendbar.
Klassische Musik bezieht ihre Vitalität auch aus dem Ansteuern verschiedener tonaler Stationen im Verlauf eines Stückes. Die Funktionsanalyse ist ein bewährtes Instrument, um eine solche Entwicklung zu veranschaulichen und Hinweise auf die jeweilige inhaltliche Bedeutung zu geben. Ihre Anwendung setzt freilich das Primat des Quintenzirkels und die Ableitbarkeit der Harmonik aus Dreiklängen voraus. Die Emanzipierung von diesem Modell intensiviert sich ab Beginn des 19. Jahrhunderts. Dabei lassen sich verschiedene, einander befruchtende Tendenzen konstatieren:
- Die Suche nach Funktionsstellvertretern bei fortgesetzter Orientierung an einer Dreiklangsbasis
- Die Gestaltung tonaler Progression mit alternativen Klängen
- Die Gestaltung von Abschnitten ohne klare tonale Orientierung
- Die Gestaltung tatsächlicher Atonalität
Da die Funktionstheorie diese Entwicklungen nicht detailliert erfassen kann wird das 19. Jahrhundert grosso modo als Zeit einer tonalen Lösung und Auflösung beschrieben, mit einem vermeintlich folgerichtigen Weitergehen zur Atonalität im 20. Jahrhundert. Die Tonalitätsanalyse mit Komplementärintervallen (im folgenden ci-Analyse; ci = complementary interval) kommt zu wesentlich differenzierteren Ergebnissen. Durch die Offenlegung der so bezeichneten tonalen Pfade lassen sich die tonalen Enigma des 19. Jahrhunderts entschlüsseln sowie der Nachweis erbringen, dass Arnold Schönberg die Komplementarität von Reihen nutzte, um bei Bedarf eine tonale Option zu implantieren und diese auch zu aktivieren.
Wer Dodekaphonie mit Atonalität gleichsetzt und daraus Kompositionsgeschichte ableitet, wird sich schwertun, in Schönbergs Kompositionstechnik die tonale Innovation zu erkennen. Auch erfordert die Auseinandersetzung mit einem neuen analytischen Instrument mehr Anstrengung als das zur Gewohnheit gewordene, freihändig-bequeme Applizieren der Etiketten tonal und atonal. Die Höhe des erforderlichen Aufwands bemisst sich am jeweiligen Ziel. Für Musikwissenschaftler ohne Theorieschwerpunkt und für ausübende Musiker muss sich der Aufwand bei der Erschließung avancierter tonaler Strukturen jedoch in Grenzen halten. An diese richtet sich dieser Leitfaden in besonderem Maße: Durch eine anwendungsorientierte Herangehensweise werden die Voraussetzungen geschaffen, um harmonisch interessante Abschnitte oder auch ganze Werke zügig durchzuanalysieren und aus der nunmehr gegebenen Evidenz der tonalen Disposition Gewinn für die Deutung respektive die eigene Interpretation zu schöpfen. Die theoretischen Grundlagen der ci-Analyse werden daher möglichst knapp abgehandelt; sie lassen sich durch die Lektüre der Theorie der Tonalität / Theory of Tonality (2013) absichern und vertiefen. Dank einer von smartmobilesolutions entwickelten Analyseapp wird das Erfassen und Auswerten der Komplementärintervalle weitgehend automatisiert und dadurch der Zeitaufwand radikal reduziert. Hierdurch wird ci-Analyse ohne großen Aufwand für jeden Musiker und Musikwissenschaftler anwendbar. Eine schrittweise Anleitung für das Arbeiten mit der App erleichtert den Zugang weiter.
Die wichtigsten Aussagen der Musik finden sich nicht auf ihrer Oberfläche. Das eigentliche Anliegen der ci-Analyse ist daher ein ästhetisches: Indem sublime harmonische Dispositionen ins Bewusstsein gehoben werden, entbinden sich Impulse zur tieferen Auseinandersetzung, zum noch genaueren Aushören und Darstellen, zur inhaltlichen Befragung. Welche Perspektiven sich hier ergeben können, werden zweckdienliche Beispielanalysen zeigen.
Die uneinheitliche Bestimmung und ungenaue Verwendung der Begriffe Tonalität und Atonalität ist Folge ausgebliebener analytischer Innovationen. Die wissenschaftliche Aporie verhindert eine angemessene Auseinandersetzung mit dem über Systemgrenzen reichenden Phänomen der Ausrichtung von Musik an Bezugstönen.
Die Verwendung der Begriffe Tonalität und Atonalität ist nicht durch eine verbindliche Definition abgesichert. Als Bezugspunkt einer terminologischen Orientierung dienen überwiegend die Dur-Moll-Tonalität sowie die aus dieser abgeleitete Kadenzharmonik. Ausgehend von deren Verfahren der tonalen Befestigung lassen sich keine Kriterien benennen, um eine sichere Abgrenzung zur postulierten Atonalität vorzunehmen. Die Aufrichtung der Dichotomie tonal/atonal ist wegen der semantisch inkorrekten Verwendung des Alpha privativum somit potenziell irreführend: Die Kompositionspraxis findet sich geprägt durch ein Kontinuum tonaler Intensitäten respektive Strukturen und nicht durch eine tonale Dichotomie.
Die beschriebene terminologische Sorglosigkeit ist Ausdruck einer tiefer reichenden Verlegenheit. Die traditionellen Werkzeuge der Tonalitätsanalyse sind aus der robusten Dur-Moll-Tonalität abgeleitet und somit nur bedingt geeignet, fragilere Strukturen zu erfassen respektive zu deuten. Die harmonischen Innovationen der Spätklassik, der Romantik und des Impressionismus lassen sich anhand der Funktions- oder der Stufentheorie daher nur rudimentär erschließen. Die entstehenden Lücken werden durch anfechtbare Deutungen und Charakterisierungen mehr überbrückt denn geschlossen. Wo der Bereich dieser deskriptiv erschlossenen tonalen Vagheit endet und in Atonalität übergeht liegt in Ermangelung abgrenzender Kriterien im Ermessen des jeweiligen Autors. Die Usus gewordenen ex cathedra-Konstatierungen von Atonalität sind daher kritisch zu sehen. Sie kaschieren die wissenschaftliche Aporie und verhindern de facto den durch die Verwendung des Begriffs suggerierten heuristischen Gewinn.
Der unreflektierte Umgang mit dem Begriffspaar Tonalität/Atonalität ist derart fest auch im wissenschaftlichen Diskurs verankert, dass die Notwendigkeit einer kritischen Auseinandersetzung kaum mehr ansatzweise erkannt wird. Besonders gravierend ist dies im Hinblick auf das Werk von Arnold Schönberg und dessen kompositionsgeschichtliche Wirkung. Schönberg hat sich zeitlebens mit der Herausforderung befasst, dass eine Weiterentwicklung von Komplexität und Ausdruck die von ihm so genannte Fasslichkeit einer Komposition erschwert. Da er ungeachtet des von ihm erhobenen hohen Gestaltungsanspruchs verstanden werden wollte, gab er das für Gliederung und Orientierung eminent wichtige Gestaltungsmittel der Tonalität mit dem Übergang zu Dodekaphonie mitnichten aus der Hand, sondern integrierte die bei Bedarf aktivierte tonale Option in Gestalt komplementärer Reihen: Komplementarität basiert auf der versteckten Symmetrie K, aus welcher sich auch die Dur-Moll-Tonalität bis ins Detail ableiten lässt. Tatsächlich nutzte Schönberg mehrfach die dadurch gegebene Möglichkeit zur Gestaltung tonaler Abschnitte, deren Sinn sich jeweils aus ihrer formalen und inhaltlichen Relevanz in einer von nicht-tonalen Teilen dominierten Faktur erklärt.
Als Pionier des nicht-tonalen Komponierens und Fortentwickler einer vom Dur-Moll-System ausgehenden Erweiterung der Tonalität lehnte Schönberg die simplifizierende Dichotomie tonal/atonal ab. Nicht die Klassifizierung vermittels eines vorgeblichen Gegensatzes sollte Gegenstand wissenschaftlicher und ästhetischer Auseinandersetzung sein, sondern ein das Dur-Moll-System übergreifendes Erfassen von tonalen Strukturen und deren Unterscheidung von tatsächlich nicht-tonalen Strukturen. Hierzu bedarf es gleichermaßen der Entwicklung geeigneter analytischer Instrumente wie der ästhetischen Sensibilisierung. Mit der Konstatierung vorgeblicher Atonalität enthebt man sich lediglich der Mühe und Verantwortung, den tonalen Weiterungen des 19. und 20. Jahrhunderts wissenschaftlich und künstlerisch gerecht zu werden.
Tonalität ist nicht an ein bestimmtes System gebunden, doch sind die gängigen Regeln zu ihrer Analyse einseitig aus der Dur-Moll-Tonalität abgeleitet. Um das Phänomen über Systemgrenzen hinweg erforschen zu können, ist neben der Kenntnis empirisch gewonnener Regeln auch die Kenntnis grundlegender Gesetzmäßigkeiten notwendig. Deren Erkundung steht die seit dem 18. Jahrhundert empirisch ausgerichtete Geschichte des Fachs Musikwissenschaft im Weg.
Die Regeln der klassischen Harmonielehre leiten sich aus der Existenz von Tonarten und Dreiklängen ab. Die Erfassung der von dieser Basis ausgehenden Erweiterung des tonalen Horizontes wird mit zunehmender Entfernung von den Grundmustern unscharf und schließlich unmöglich. Arnold Schönberg kritisierte dies in seiner im Jahr 1911 erstmals publizierten Harmonielehre und forderte ein System, welches auf Naturgesetzen basieren solle. Im gleichen Atemzug gab er an, entsprechende Grundsätze selber (noch) nicht gefunden zu haben. Mit der von ihm benannten Herausforderung ringt das Fach noch ein gutes Jahrhundert später: In tonal avancierten Kompositionen wird die analytische Auseinandersetzung mit zunehmender Subtilität und Fragilität der tonalen Disposition prinzipiell immer wichtiger, während zugleich deren Darstellung anhand der tradierten Methoden immer fragwürdiger scheint.
Die Musikwissenschaft hat sich zu dieser Herausforderung in eigentümlicher Weise verhalten. Obgleich eine verbindliche Definition des Begriffes Tonalität nicht existierte (und weiterhin nicht existiert), setzte man ohne Benennung eines abgrenzenden Kriteriums die Atonalität als Gegensatz. Da sich viele klangliche Phänomene keinem der beiden Begriffe sicher zuordnen ließen, kreierte man für den Bereich zwischen den Gegensätzen Tonalität und Atonalität weitere Begriffe wie den der schwebenden oder der aufgehobenen Tonalität. Bei der konkreten Anwendung dieser Terminologie sucht man vergeblich nach stichhaltigen Begründungen: Das Etikett Atonalität ziert vornehmlich Kompositionen, welche mit den überkommenen analytischen Verfahren nicht erschlossen werden können; serielle und dissonanzreiche Werke sind bevorzugte Gegenstände solcher Zuordnung. Zudem lässt die durch das Alpha privativum aufgerichtete Dichotomie eigentlich kein Drittes in Gestalt eines tonalen Zwischenbereichs zu. Statt zum Verständnis tonaler Entwicklungen beizutragen wird durch die Verengung des Diskurses auf die Dichotomie tonal/atonal eine Auseinandersetzung gemieden und Erkenntnis verhindert.
Bei der Suche nach Gründen für das Ausbleiben analytischer Innovationen hilft ein Blick auf die Geschichte der Musiktheorie. In der Antike wurde diese, gemeinsam mit Arithmetik, Geometrie und Astronomie, dem mathematisch ausgerichteten Quadrivium zugerechnet. Die Konzentration auf grundlegende Fragestellungen setzte sich im Mittelalter fort. Dies limitierte die Möglichkeiten, die Entwicklungen und Umbrüche der abendländischen Musikgeschichte zu erfassen und zu reflektieren. Ein Paradigmenwechsel hin zur konkreten Arbeit am Werk brachte die Musiktheorie wieder auf die Erfolgsspur, verlagerte zugleich den Schwerpunkt der Auseinandersetzung vom Grundsätzlichen und Abstrakten hin zum Empirischen. Die nunmehr aus vorgefundenen Kompositionen abgeleiteten und sodann auf diese wiederum angewendeten Regeln besitzen Relevanz innerhalb eines Tonsystems respektive innerhalb eines begrenzten historischen Zeitraums, jedoch keine Allgemeingültigkeit.
Das Streben nach tonaler Orientierung manifestiert sich über Epochen-, System- und Kulturgrenzen hinweg in vielgestaltiger Weise. Bei den Kirchentönen entscheiden, bei gleichbleibendem Material, die Struktur des Melos respektive die Festlegung des Ambitus über die Zuweisung tonaler Bedeutung. Die melodische Begründung der Tonalität wird im historischen Verlauf durch eine harmonische ergänzt. Fluchtpunkt dieser Entwicklung ist die auf Dreiklängen basierende Harmonik der Klassik. Das 19. Jahrhundert schreitet von hier fort zu oft nicht mehr aus Dreiklängen ableitbaren Vielklängen; sodann versucht Arnold Schönberg in einigen seiner komplementären Reihen eine tonale Option zu implantieren und von dieser auch Gebrauch zu machen. Die aus der Dur-Moll-Tonalität abgeleiteten Analysemethoden vermögen tonale Prozesse am Rande oder jenseits der Grenzen dieses Systems nicht angemessen zu erfassen und zu bewerten. Zu ihrem Verständnis ist daher die von Schönberg geforderte, Systemgrenzen übersteigende Kenntnis der zugrundeliegenden Gesetzmäßigkeiten unabdingbar. Ein Bewusstsein für die Notwendigkeit, entsprechend abstrahierende analytische Kompetenzen zu entwickeln, ist in der überwiegend auf das Erfolgsmodell der empirischen Arbeit am Werk fokussierten Musikwissenschaft jedoch kaum ausgeprägt. An die Stelle tatsächlicher Auseinandersetzung mit dem Phänomen Tonalität ist daher das Narrativ ihrer Auflösung im 19. Jahrhundert getreten, welche im 20. Jahrhundert durch Arnold Schönbergs Übergang zur Atonalität vollendet worden sei. Schönberg hat vehement gegen die Gleichsetzung von Atonalität und Dodekaphonie argumentiert, sich aber offenbar nicht bereit gefunden, auch nur seine engsten Schüler über die von ihm gewonnenen und ins Werk gesetzten Erkenntnisse zur Steuerung harmonisch-tonaler Prozesse im Zwölftonraum in Kenntnis zu setzen. Apologeten und Wissenschaftler haben sich daher nie mit Schönbergs Technik befasst, in seriellen Kompositionen Atonalität und systemisch abgesicherte Tonalität in Beziehung zu setzen. Die einseitig auf die atonale Komponente gerichtet Rezeption seines Schaffens hat der Musikwissenschaft, der Musiktheorie und der Kompositionsgeschichte einen weiteren, beachtlichen Umweg beschert.
Klänge modellieren den tonalen Möglichkeitsraum. In dem Maße, wie das Erreichen konkreter tonaler Ziele ästhetisch und inhaltlich an Bedeutung verliert, werden die Auseinandersetzung mit der durch die Klänge generierten Raumstruktur und die tonalen Bewegungsrichtungen erkenntnisleitend.
Die konventionellen Werkzeuge zur Analyse tonaler Strukturen sind Ausdruck einer spezifischen Ästhetik. Diese beruht auf der Vorstellung eines harmonischen Gleichgewichts, welches gelegentlich – insbesondere durch Dissonanzen – heftig irritiert, jedoch nicht suspendiert wird. In der klassischen Musik ist die Tonika Symbol und tonales Ziel dieser letztlich gewahrten Balance. Nicht ohne Grund wird die einschlägige Auseinandersetzung mit Klangfolgen als Harmonielehre bezeichnet. Der Vorstellung harmonischer Proportionen respektive Beziehungen hat die Architektur, Kunst, Geistes- und Naturwissenschaften über mehrere Epochen hinweg prägend beeinflusst. Dies gilt auch in ihrer Negation, wenn der Verlust eines Gleichgewichts als solcher empfunden und gestaltet wird. In der Musik zieht besonders das romantische 19. Jahrhundert aus dieser Möglichkeit Gewinn. Da wird Liebeskummer durch die Entkernung der tonalen Mitte ins Werk gesetzt, veranschaulicht das Wegspringen in eine entfernte Tonart Entfremdung oder Verrücktheit. Die Musikwissenschaft sucht die Ergebnisse traditionell und ausdauernd mit Hilfe zweier komplementärer Antonyme zu deuten: Es sind dies die Gegensatzpaare Konsonanz/Dissonanz und Tonalität/Atonalität.
Arnold Schönberg hat mit der Konstatierung der Emanzipation der Dissonanz eine Entwicklung beschrieben, an deren Ende sich klangliche Prozesse nicht mehr aus der Wechselbeziehung gegensätzlicher Klangklassen deuten lassen. In dem Maße, wie Dissonanzen als eigenständige Phänomene wahrgenommen wurden, verlor die dichotomische Klassifizierung von Konsonanzen und Dissonanzen an Relevanz.
Von Anbeginn problematisch war die Einführung des Begriffes Atonalität. Tonalität ist kein durch eine klar abgrenzende Definition abgesicherter Begriff, weshalb die durch das Alpha privativum postulierte Dichotomie zur Klassifizierung nicht genügt. Die Einordnung von Kompositionen als tonal oder atonal ist daher oft willkürlich und führt selten zu einem Erkenntnisgewinn. In der Praxis wird die formale Dichotomie tonal/atonal ohnehin als Polarität behandelt, erscheinen Tonalität und Atonalität als Fluchtpunkte eines nuancierten Ereignisraums. Die üblichen Charakterisierungen der in diesem Raum wahrgenommenen Prozesse, beispielsweise als „schwebend“ oder „vagierend“ (Schönberg) ermöglichen in ihrer Unverbindlichkeit keine detaillierte Aussage zur jeweiligen Ausdrucks- oder Aussageintention.
Es gilt, die veränderte ästhetische Situation zu reflektieren und die Folgen für eine analytische Auseinandersetzung zu bedenken. In avancierten harmonischen Strukturen sind potentielle tonale Ziele Gestaltungsmittel, aber nicht mehr notwendig Fluchtpunkt der Entwicklung. Bewegungen im tonalen Möglichkeitsraum sind hinsichtlich ihrer Ausrichtung keiner Wertung mehr unterworfen. Die Verengung dieses Raums infolge des Fortfalls tonaler Optionen kann ohne Weiteres vor dem Erreichen eines tonalen Ziels angehalten und umgekehrt werden. Entwicklungen können abbrechen, oder sich durch die Einführung tonal ungerichteter Abschnitte verzögern. Eine dichotomische Klassifizierung solch heterogener Prozesse ist ersichtlich nicht zielführend. Auch eine Analyse mithilfe der aus Skalen und Dreiklängen abgeleiteten Funktions- oder der Stufentheorie stößt bald an eine Grenze, weil die Privilegierung einer bestimmten Tonauswahl oder bestimmter Klänge in tonal avancierten Kompositionen nicht vorausgesetzt werden kann.
Da das Erreichen eines tonalen Zieles in einer avancierten Komposition nur eine Option und keine Bedingung ist, kann ein solches Ziel nicht länger exklusiver Bezugspunkt einer dem Gegenstand angemessenen Analyse sein. Diese muss die Modifikationen des Möglichkeitsraumes erfassen und daher mit umgekehrten Vorzeichen arbeiten. Es wird kein Ziel postuliert, sondern zunächst festgestellt, welche tonalen Ziele durch einen Klang respektive eine Klangfolge obsolet werden: Aus der Synopse der jeweiligen Restriktionen ergibt sich sodann die jeweils aktuelle Struktur des Möglichkeitsraumes. Wie zu zeigen sein wird, indizieren Komplementärintervalle präzise den Wegfall tonaler Optionen. Sie eignen sich daher in besonderen Maße, um komplexere tonale Prozesse zu erfassen und einer analytisch fundierten Deutung zugänglich zu machen. Dabei ist es unerheblich, ob ein Klang nach herkömmlicher Klassifizierung konsonant oder dissonant ist oder aus einem Dreiklang abgeleitet werden kann. Die auf der Erfassung von Komplementärintervallen fußende ci-Analyse macht sichtbar, welche tonalen Pfade durch Klangfolgen modelliert werden. Sie ist daher prädestiniert für die Auseinandersetzung mit komplexen harmonischen Prozessen.
Harmonische Tonalität ist das Resultat einer zweckdienlichen Reihung von Klängen. Im Verlauf dieser tonalen Progression scheiden sukzessive potentielle Ziele aus. Am Ende einer solchen Entwicklung steht oft, aber nicht zwingend, die verbindliche Ausrichtung auf ein tonales Zentrum.
Harmonische Tonalität ergibt sich aus einer zweckdienlich-planvollen Reihung von Klängen. Die Standardkadenz (T S D T) ist Paradigma eines solchen, hier auf tonale Zentrierung gerichteten Prozesses, die Funktionstheorie das maßgeschneiderte Mittel seiner Analyse und Darstellung. Eine Kadenz beschneidet sukzessive die Anzahl tonaler Optionen, bis nur ein Ziel übrig bleibt. Sie kann sich hierfür auf die Töne der dem Ziel zugeordneten Tonleiter beschränken. Besonders ab dem 19. Jahrhundert emanzipierte sich die Kompositionspraxis in zweifacher Hinsicht von diesem Modell. Zum einen kamen bei der Suche nach klanglicher Orientierung zunehmend tonleiterfremde Töne ins Spiel; hinzu kamen tonale Alternativen, die sich nicht vollständig aus Dreiklangsmodellen ableiten lassen. Zum anderen entwickelten sich Ausdrucks- und Aussageintentionen, welche sich in der Abgeschlossenheit einer tonikalen Welt nicht darstellen lassen: Offenheit, Ungewissheit, Verlorenheit oder Enthobenheit; Brüche, Umschwünge, Abstürze, Ver- und Entrücktheit.
Neben der Ausrichtung auf ein tonales Ziel werden daher weitere Optionen tonaler Gestaltung relevant. So können am Ende einer harmonischen Entwicklung zwei potentielle tonale Ziele übrig bleiben; häufige Perspektivenwechsel ohne finale Ausrichtung auf ein Ziel oder abrupte Wechsel des tonalen Bezugsrahmens können den Möglichkeitsraum bis hin zur quasi orientierungslosen Offenheit weiten, verdichtete Klänge jede Perspektive vernichten.
Um einen Ausgangspunkt zur Erschließung tonal avancierter Modelle zu finden ist es hilfreich, zunächst die Möglichkeiten und Grenzen der konventionellen Funktionsanalyse zu betrachten. Diese konzentriert sich auf das Modell einer letztendlichen Hinordnung der tonalen Progression auf ein tonales Zentrum. Dabei gelingt es ihr, eine auch inhaltlich oft aussagekräftige Hierarchie tonaler Nebenschauplätze aufzurichten und dank der Zusammenfassung verschiedener Klänge zu Funktionsgruppen Übersichtlichkeit zu schaffen. Die Zuweisung einer Funktion klammert freilich das über diese hinausgehende Potential eines Klanges weitgehend aus. Eine Funktionsbezeichnung erfasst beispielsweise, dass eine Subdominante in Moll oder Dur gesetzt ist, deren Quint durch eine Sexte ergänzt oder ersetzt wird. Sie trifft jedoch keine Aussage darüber, wie sich der nachgeordnete Möglichkeitsraum durch die Entscheidung für einen bestimmten Funktionsvertreter ändert. Tatsächlich ist den intrinsischen Qualitäten einer Funktion bereits in klassischer Musik Bedeutung zuzumessen: So ist im Vorfeld einer Modulation zur Dominante die Ersetzung der Standardsubdominante durch eine s6 respektive S6 zweckdienlich (Öffnung des Dominantraums), eine sixte ajoutée hingegen nicht. Die empirisch festgestellte Privilegierung eines Klanges in einem spezifischen Kontext kann einen Hinweis auf den nachgeordneten Möglichkeitsraum geben. Sie vermag jedoch nicht dessen Beschaffenheit zu konkretisieren und detailliert zu begründen. Vollends problematisch wird es, wenn tonal relevante Klänge sich funktional nicht mehr zuordnen lassen, respektive gegebene Zuordnungsmöglichkeiten keine Entsprechung im ästhetischen Erleben finden.
Um einen Zugang zu finden, bedarf es somit eines analytischen Antagonisten. Einer Methode, welche zunächst die Frage nach dem hypothetischen Ziel ausklammert, aber eruiert, welche Ziele nicht mehr erreicht werden können.
Harmonisch tonale Prozesse im Zwölftonraum sind systemübergreifend ableitbar aus der versteckten Symmetrie K. Dass diese Rückgrat der komplementären Zwölftonreihen Schönbergs wie auch der Dur-Moll-Tonalität ist, zeigte sich im Verlauf der auf ihre Entdeckung folgenden Auseinandersetzung. Diese mündete in die Entwicklung einer Methode der Tonalitätsanalyse vermittels der Erfassung und Zuordnung von Komplementärintervallen.
Die Geschichte der ci-Analyse begann mit der Entdeckung, dass Arnold Schönberg zur Generierung seiner komplementären Reihen eine versteckte, fortan mit „K“ bezeichnete Symmetrie nutzte (Stegemann, 2003). K lässt sich veranschaulichen, indem man an beliebiger Stelle im chromatischen Total eine Spiegelachse setzt. Im nachstehenden Beispiel liegt diese zwischen den Tönen h und c, was hinsichtlich der Abbildungsverhältnisse übrigens zu identischen Ergebnissen führt wie eine Setzung zwischen f und f#:
f# g g# a b h | c c# d d# e f
Im konkreten Fall ist der Ton f Symmetriepartner von f#, e derjenige von g, oder mathematisch ausgedrückt: f = K(f#), e = K(g) … c = K(h). Bei einer evidenten Symmetrie sind die Symmetriepartner unmittelbar nachvollziehbar (sichtbar) aufeinander bezogen. Bei der Symmetrie K verhält es sich hingegen so, dass ein Ton x und sein Komplement K(x) voneinander getrennt werden, beispielsweise durch die Zuordnung zu verschiedenen Tonmengen. In einer komplementären Zwölftonreihe wird diese Trennung dadurch erreicht, dass die Setzung eines Tones im 1. Hexachord die Setzung seines Komplements im 2. Hexachord bedingt. Dies lässt sich beispielsweise bei der Betrachtung der Reihe von Schönbergs Klavierkonzert op. 42 leicht nachvollziehen.

Die K-Achse der Reihe liegt zwischen den Tönen h und c (respektive f und f#). Komplement des 1. Reihentones (RT) eb ist der 8. Reihenton g#, Komplement des 2. Reihentons b ist der 9. Reihenton c#. d = K(a) (RT 10), f (RT 4) = K(f#) (RT 7), e (RT 5) = K (g) (RT 12) und c (RT 6) = K(h) (RT11). Die Komplemente der Reihentöne 1 bis 6 liegen somit durchweg im zweiten Hexachord. Dies wird durch Färbung der Töne des 1. Hexachords im chromatischen Total anschaulich. Jeder rot gefärbte Ton wird durch K auf einen nicht gefärbten abgebildet:
f# g g# a b h | c c# d eb e f
Dieses Ordnungsprinzip gilt für sämtliche komplementären Reihen, wobei jeweils die Lage von K im chromatischen Total zu eruieren ist.
Durch die Betrachtung einer Reihenoberfläche oder das Spielen der Reihentöne lässt sich K nicht ermitteln, zumal die Töne innerhalb eines Hexachords beliebig umgestellt werden können, ohne die Komplementarität einer Reihe aufzuheben. Solche Abwesenheit evidenter Symmetrie dürfte ursächlich dafür sein, dass K so lange unentdeckt blieb. Wäre K lediglich das Ordnungsprinzip für komplementäre Reihen, ergäben sich aus solcher Unkenntnis keine weiter reichenden Folgen. Während der Beschäftigung mit der Gesetzmäßigkeit fiel jedoch auf, dass Schönberg gelegentlich innerhalb einer K-Struktur den zweiten Ton links der K-Achse respektive dessen Tritonustransposition tonal privilegierte, eine latente Tonikalität ins Werk setzte. In op. 42 betrifft die tonale Privilegierung den Ton b. Diese ist in Gestalt des durch die Reihentöne 3-5 modellierten B-Dur-Dreiklangs auch auf der Reihenoberfläche sichtbar. Bei einem Komponisten, der kaum jemals etwas dem Zufall überließ, regte dies weitere Auseinandersetzung an. Sie mündete zunächst in die Beobachtung, dass auch eine klassische Standardkadenz (T S D T), Kernelement eines ganz anders gearteten Zwölftonsystems, K-kompatibel ist (Mazzola/Stegemann, 2007). Hier bedarf es zunächst einer Erläuterung, was Kompatibilität in diesem Kontext bedeutet:
- Da es nach sechs Halbtonverschiebungen im chromatischen Total wieder zu identischen Abbildungsverhältnissen kommt, lassen sich durch das Einsetzen von K sechs verschiedene K-Strukturen im chromatischen Total generieren.
- Von Komplementarität sind nur die Intervallklassen kleine Sekunde, kleine Terz und Quart sowie die sie zur Oktave ergänzenden Klassen große Septime, große Sexte und Quinte betroffen. Also jene Intervalle, welche durch eine zwischen zwei Töne des chromatischen Totals aufgerichtete Symmetrieachse generiert werden.
- Im beispielhaften Durdreiklang b-d-f sind somit die Intervalle b-f und d-f in bestimmten K-Strukturen komplementär.
- Bei einer Platzierung der K-Achse beispielsweise zwischen den Tönen h und c (respektive f und f#) generiert keines der in den Dreiklängen von B-, Es- und F-Dur (der Tonika, Subdominante und Dominante von B-Dur) enthaltenen Intervalle ein Komplement. In jeder der anderen fünf K-Strukturen ist wenigstens eines dieser Intervalle komplementär. Daraus folgt, dass beispielsweise die B-Dur-Kadenz nur in der K-Struktur mit der zwischen den Tönen h und c (respektive f und f#) platzierten Achse modelliert werden kann. Die Tonart B-Dur lässt sich somit verbindlich dieser Struktur zuordnen. Eine solche Zuordnungsmöglichkeit existiert für jede der zwölf Dur- und der zwölf Molltonarten.
Die vergleichende Untersuchung der Kadenzharmonik mit Schönbergs serieller Technik verwies auf eine grundlegende Bedeutung der Komplementarität im Hinblick auf die tonale Orientierung im Zwölftonraum. Damit war es erstmals möglich, eine Regelmäßigkeit der tonalen Stabilisierung durch Akkordfolgen nachzuweisen, die zwei verschiedene Tonsysteme miteinander verbindet:
Ein Komplementärintervall schließt die ihm zugeordnete Tonstruktur als Ort tonaler Zielsetzung aus. Durch die Aufeinanderfolge zweckdienlicher Klänge werden sukzessive K-Strukturen ausgeschlossen, bis nur eine übrig bleibt. Diese Ausrichtung auf eine einzige K-Struktur ist Voraussetzung einer tonalen Befestigung und nicht auf ein bestimmtes Tonsystem beschränkt.
In der Auseinandersetzung mit den Implikationen der Komplementarität klären sich zentrale Fragestellungen zur Dur-Moll-Tonalität, ihrer Erweiterung besonders im 19. Jahrhundert, sowie zur Integration der tonalen Option in die Dodekaphonie Schönbergs. Eine Tonart wird über ihren Tonvorrat – die siebenstufige Skala – und die aus diesem abgeleiteten Dreiklänge definiert. Dennoch tragen die fünf übrigen, der Tonleiter nicht inhärenten Töne gelegentlich zur klanglichen Entwicklung bei. Zum einen geschieht dies wie zu erwarten zur bewussten und wirkungsvollen Verzögerung der tonalen Befestigung. Zugleich können tonartfremde Töne auch zur Progression beitragen, und mit der Erweiterung der Tonalität im 19. Jahrhundert werden ganze Klänge aus fremden Kadenzzusammenhängen in die tonale Entwicklung integriert. Der vermeintliche Widerspruch löst sich auf, wenn man Bewusstheit darüber erlangt, dass für die Ausrichtung auf eine K-Struktur die verwendeten Komplementärintervalle verantwortlich sind. Die mögliche Zugehörigkeit der Intervallbestandteile zum Tonvorrat der Zieltonart ist für diese Ausrichtung irrelevant. Sie kommt mit dem nächsten Schritt ins Spiel: Da jede K-Struktur Basis von jeweils zwei Dur- und zwei Molltonarten ist (Näheres hierzu im folgenden Kapitel), bedarf es der Einengung des Tonvorrats zwecks Bestätigung der Zieltonart. Die Befestigung einer Tonart ist somit ein in zwei Teile zu gliedernder Prozess:
- Schritt I: Durch die Generierung von zweckdienlichen Komplementärintervallen erfolgt die Ausrichtung auf eine bestimmte K-Struktur.
- Schritt II: Durch die Verringerung des Tonvorrats erfolgt die Ausrichtung auf eine der vier Tonarten der ausgewählten K-Struktur.
Im Interesse einer zügigen Befestigung der Tonart legiert die klassische Harmonik die beiden Schritte, verbindet die Ausrichtung auf die jeweilige K-Struktur mit einer weitgehenden Beschränkung auf den Tonvorrat der Zieltonart. Die aus der klassischen Harmonik abgeleiteten Analysemethoden – Funktions- und Stufentheorie – setzen diese Legierung voraus. Die harmonischen Verfahren des 19. Jahrhunderts zielen hingegen häufig auf eine Verzögerung der tonalen Entscheidung oder gar deren Verweigerung. Um Solches ins Werk zu setzen bedarf es der Aufeinanderfolge besagter Schritte. Leider sind Funktions- und Stufentheorie nicht geeignet, den Teil einer harmonischen Abfolge, der auf dem ersten Schritt beruht, isoliert zu erfassen und dann zu interpretieren. Der eminente Vorzug der ci-Analyse gründet darin, diesen Teil der Progression sichtbar zu machen, die Eingrenzung des tonalen Möglichkeitsraums durch Komplementärintervalle präzise abzubilden. Infolgedessen lösen sich zahlreiche Enigma der romantischen und impressionistischen Harmoniesprache in Wohlgefallen auf: Sie erklären sich aus der Reduzierung des tonalen Möglichkeitsraums durch Komplementärintervalle (Schritt I), ohne dass durch eine zweckdienliche Einschränkung des Ton- respektive Dreiklangsvorrats bereits das tonale Ziel kenntlich gemacht worden wäre. Dies Ausrichtung auf das Ziel erfolgt – wenn überhaupt – erst mit dem nunmehr nachgelagerten Schritt II.
Die Auseinandersetzung mit den Gesetzmäßigkeiten eines durch K strukturierten Zwölftonraums aktualisiert die Erkenntnisse hinsichtlich der grundlegenden Bedeutung des Dreiklangs. Im 19. Jahrhundert gelingt es, die harmonische Progression in Grenzen von diesem zu emanzipieren. Da nach der Ausrichtung auf einen der sechs K-Strukturen immer noch vier potentielle tonale Ziele existieren, behält die Bindungskraft des Dreiklangs im Hinblick auf auf die tonale Bestätigung gleichwohl auch in harmonisch avancierten Kompositionen ihre Bedeutung. Arnold Schönberg ist bestrebt, die Emanzipierung vom Dreiklang noch weiter voranzutreiben. Sein Leitgedanke des Komponierens mit zwölf nur aufeinander bezogenen Tönen findet in seinem Werk jedoch keine uneingeschränkte Entsprechung. Da er beinahe ausschließlich mit komplementären Reihen arbeitet, stehen ihm von den 924 möglichen Dichotomien zur Aufteilung des chromatischen Totals in Hexachorde lediglich die zwanzig mit komplementärer Struktur zur Verfügung, von denen er tatsächlich 15 verwendet. Schönberg sieht sich wie bereits vor ihm die Romantiker und die Impressionisten mit der Herausforderung konfrontiert, dass sich jede Erweiterung im tonalen Möglichkeitsraum mit einer Abnahme der Nachvollziehbarkeit verbindet.Tatsächlich bleiben durch die Konzentration auf die Komplementarität etwa 98% der Dichotomien ungenutzt, ist die Erweiterung des Möglichkeitsraums angesichts des von Schönberg erhobenen Anspruchs überschaubar. Und angesichts der tonalen Konkurrenz in einem Tonraum unter K findet sich auch noch bei Schönberg die Tendenz, bei Kompositionen mit tonaler Implikation Dichotomien zu verwenden, bei denen die Dreiklangsbestandteile der latenten Tonika sich in einem Hexachord zusammenfinden. Im Klavierkonzert op. 42 wird dieser Dreiklang in Gestalt der Reihentöne 2 bis 4 sogar auf der Reihenoberfläche exponiert. Selbst in seriellen Kompositionen bleibt der Dreiklang das effektivste Mittel zur Affirmation eines tonalen Ziels.
Wie noch zu zeigen sein wird, nutzt Schönberg seine seriellen Techniken bei Bedarf gezielt zur Modellierung tonal gerichteter Abschnitte respektive Formteile. Wo er dies tut, sind seine Schöpfungen in gleicher Weise der Gesetzmäßigkeit der Komplementarität unterworfen wie zuvor schon Dur-Moll-tonale Kompositionen. Die durch ci-Analyse sichtbar werdenden tonalen Pfade dokumentieren dies eindrucksvoll.
Quellen:
- Mazzola, Guerino & Stegemann, Benedikt: Hidden symmetries of classical tonality in Schönberg’s dodecaphonic compositions, in: Journal of Mathematics & Music, p. 37-51, Oxon, 2007
- Stegemann, Benedikt: Arnold Schönbergs musikalische Gedanken, Frankfurt, 2003
- Stegemann, Benedikt:Theorie der Tonalität / Theory of Tonality, Wilhelmshaven, 2013
Harmonisch-tonale Prozesse im Zwölftonraum lassen sich über Systemgrenzen hinweg durch die Erfassung und Zuordnung von Komplementärintervallen offenlegen. Dank der Entwicklung einer zweckdienlichen App wurde dieser an sich zeitaufwendige Vorgang radikal vereinfacht und beschleunigt. Um das Verfahren zu verstehen, bleibt eine Auseinandersetzung mit der grundlegenden Gesetzmäßigkeit gleichwohl unerlässlich.
Wie im vorigen Kapitel angedeutet, werden durch die sukzessive Verschiebung der Achse K im chromatischen Total sechs verschiedene K-Strukturen generiert. Grundeigenschaft von K ist die Trennung der Symmetriepartner: Die Setzung eines Tons x führt zum Ausschluss seines komplementären Symmetriepartners K(x). Der Ausschluss bezieht sich auf ein mögliches Zusammenklingen, gestattet das Erscheinen von x und K(x) in zeitlicher Abfolge. Die Abbildungsverhältnisse der sechs, nunmehr von I bis VI durchnummerierten K-Strukturen finden sich in nachfolgender Tabelle:
Das Wirkungsprinzip der ci-Analyse lässt sich vermittels der Betrachtung der Standardkadenz beispielsweise von C-Dur veranschaulichen. Der Tonikadreiklang c-e-g enthält das Komplementärintervall c-g aus der K-Struktur III sowie das Intervall e-g aus Struktur V. K III und K V scheiden somit als möglicher Ort einer tonalen Befestigung aus, da die genannten Intervalle in diesen Strukturen jeweils nicht zulässig sind. Die Subdominante f-a-c enthält das Intervall f-c aus K VI und das Intervall a-c aus K II, die Dominante g-h-d das Intervall g-d aus K II und das Intervall h-d aus K IV. Die Standardkadenz von C-Dur generiert somit Komplementärintervalle in den K-Strukturen II, III, IV, V und VI. Ihre tonale Basis ist K I. Das Offenbleiben einer K-Struktur (hier K I, blau markiert) in einer harmonischen Progression wird im Folgenden als tonaler Pfad bezeichnet.
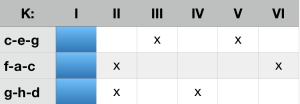
Tonaler Pfad der C-Dur-Standardkadenz
Die nachfolgende Tabelle zeigt in der Übersicht, welcher Dreiklang in welcher K-Struktur ein Komplementärintervall generiert. Eine Übersicht über die Realisierbarkeit (+) oder Nichtrealisierbarkeit (-) aller Dur- und Molldreiklänge in den sechs K-Strukturen in Synopse macht evident, dass jede Kadenz exklusiv in einer K-Struktur realisiert werden kann, und jede K-Struktur Basis für jeweils zwei Dur- und Molltonarten ist. In K I sind dies die Kadenzen von C-Dur (rot) und Fis-Dur (blau), von d-Moll (rot) und as-Moll (blau):
Durdreiklänge
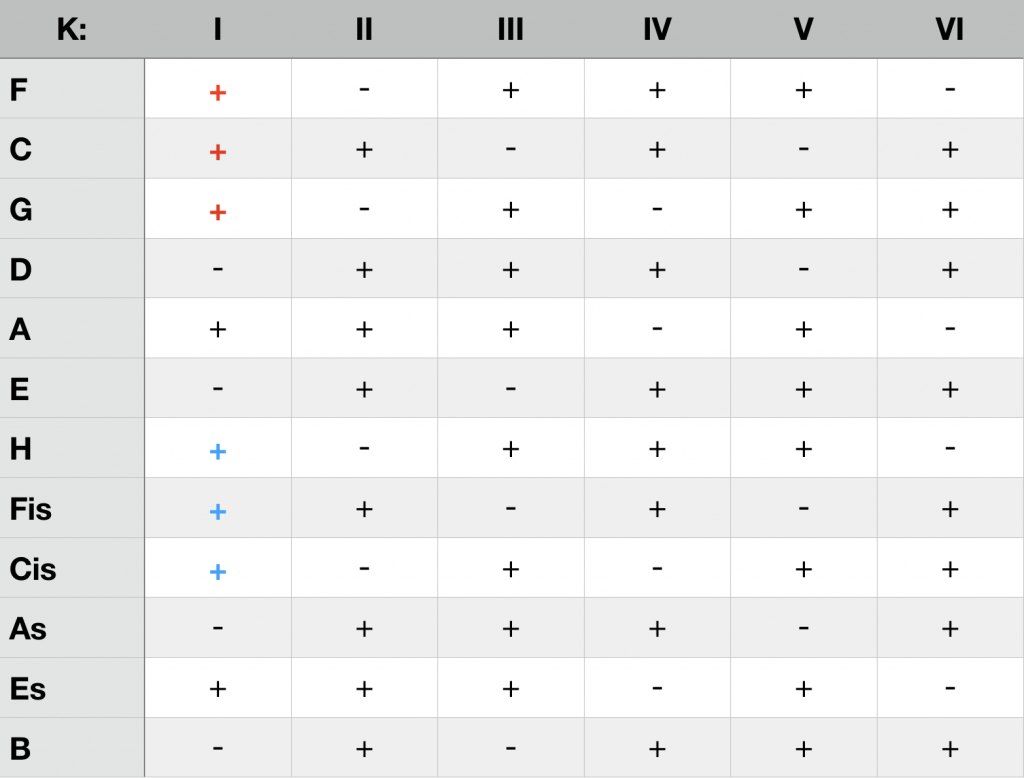
Molldreiklänge
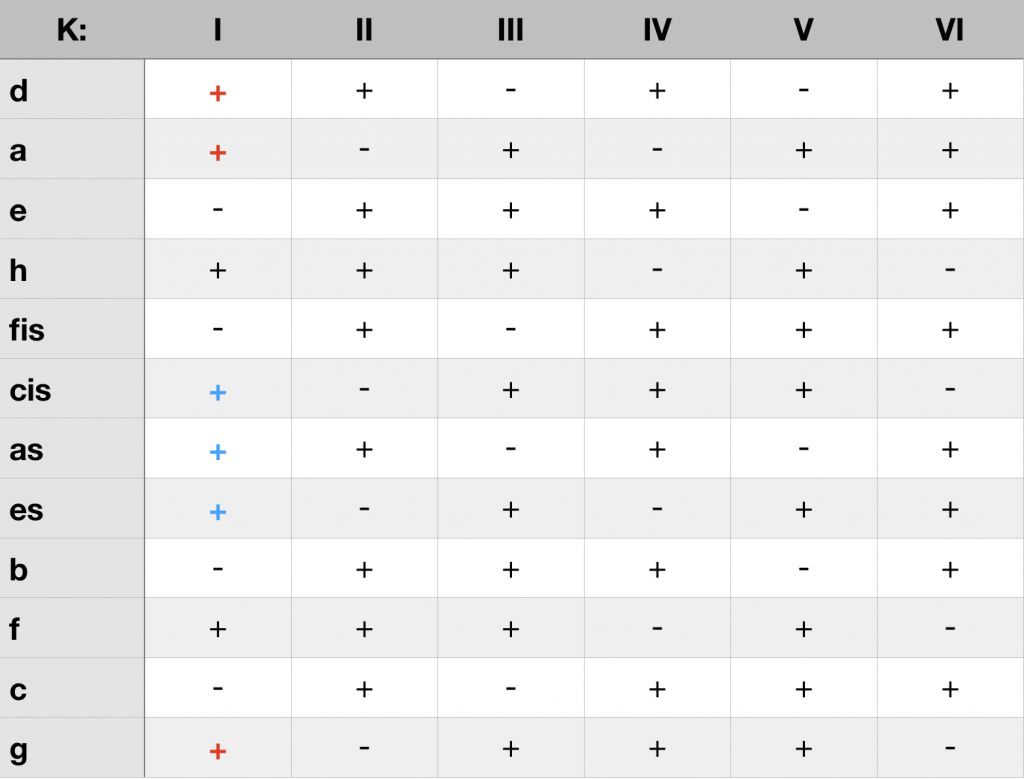
Anhand der Dreiklangstabellen lässt sich jeder Kadenz und somit jeder Tonart eine K-Struktur zuweisen. Die nachfolgende Tabelle gibt einen Überblick über die Zuordnungen sowie die in der jeweiligen Struktur nicht zulässigen, da dort komplementären Intervalle.
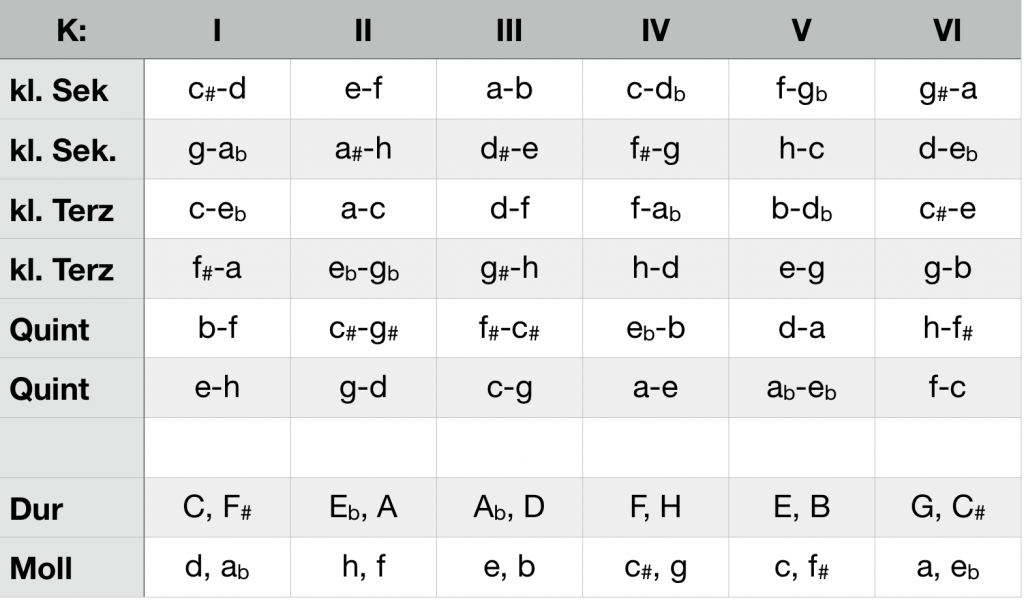
ci und Tonarten der sechs K-Strukturen
In der harmonisch avancierten Musik des 19. und 20. Jahrhunderts lässt sich die tonale Progression partiell nicht mehr aus Dreiklängen ableiten. Sie erschließt sich jedoch, wenn man die in der Tabelle gelisteten Komplementärintervalle aus vorgefunden Klängen extrahiert und infolge ihrer Zuordnung zu einer K-Struktur den jeweiligen Beitrag zur Modellierung des tonalen Möglichkeitsraumes eruiert. Aus der Auflistung der von den Komplementärintervallen generierten Ausschlüsse in Tabellen ergibt sich ein Überblick über die tonale Progression. Da beispielsweise bei einem Fünfklang zehn Intervallbeziehungen untersucht und ggf. zugeordnet werden müssen, ist der Aufwand jedoch sehr hoch und fehleranfällig. Durch das Arbeiten mit der ci-App wird die Analyse auf eine neue Grundlage gestellt, da nach der Eingabe der Töne eines Klanges die Auswertung und die tabellarische Aufbereitung automatisch ablaufen. Das konkrete Procedere ist Gegenstand mehrerer Tutorials.
Die zentralen harmonischen Prozesse der Klassik können mit der hierfür maßgeschneiderten Funktionstheorie gut beschrieben werden. Gleichwohl vertieft ci-Analyse das Verständnis und gibt Aufschluss im Detail. Nachfolgend einige, zum Teil im Tutorial Klassik eingehender erläuterte Beispiele:
- In der C-Dur Kadenz exkludiert lediglich das im Subdominantdreiklang enthaltende Intervall f-c die K-Struktur der Dominante (K VI). Bei einer Entscheidung für die Funktionsvertreter S6, s6 und sn bleibt K VI daher offen. In Kenntnis des Sachverhalts lässt sich empirisch die Häufigkeit das Auftretens insbesondere eines S6 oder s6 im Kontext einer Modulation zur Dominante überprüfen.
- Im Akkord g-h-d-f-a steht das Intervall d-a- einer tonalen Befestigung in K V entgegen, bei g-h-d-f-ab das Intervall g-ab einer Befestigung in K I. Die Hinzufügung einer großen None zu einem Dominantseptakkord verneint somit die Möglichkeit einer nachfolgenden Molltonika, die Hinzufügung einer kleinen None eine Durtonika. Dies wird in der kompositorischen Praxis genau beachtet.
- Die Funktion Dp generiert ein Komplementärintervall in der K-Struktur der Tonika. Im Fall von C-Dur ist dies das Intervall e-h in K I. Tatsächlich spielt diese Funktion im Kontext einer tonalen Befestigung der Tonika keine Rolle.
- Die sixte ajoutée wird als charakteristische Dissonanz der Subdominante bezeichnet, die kleine Septime als diejenige der Dominante. Charakteristisch kann der Zusatz notabene nur dann sein, wenn er in der K-Struktur der Tonika nicht gleichermaßen der Dominante wie der Subdominante zugewiesen werden kann. Die sixte ajoutée ist der einzige Zusatz zum Grunddreiklang, welcher diese Voraussetzung bei der Subdominante unabhängig vom Tongeschlecht erfüllt, im Falle der Dominante ist es die kleine Septime.
Die nachfolgende Tabelle gibt einen Überblick der von verschiedenen Funktionsvertretern generierten Exklusionen. Die im besprochenen Kontext relevante ist jeweils rot markiert.
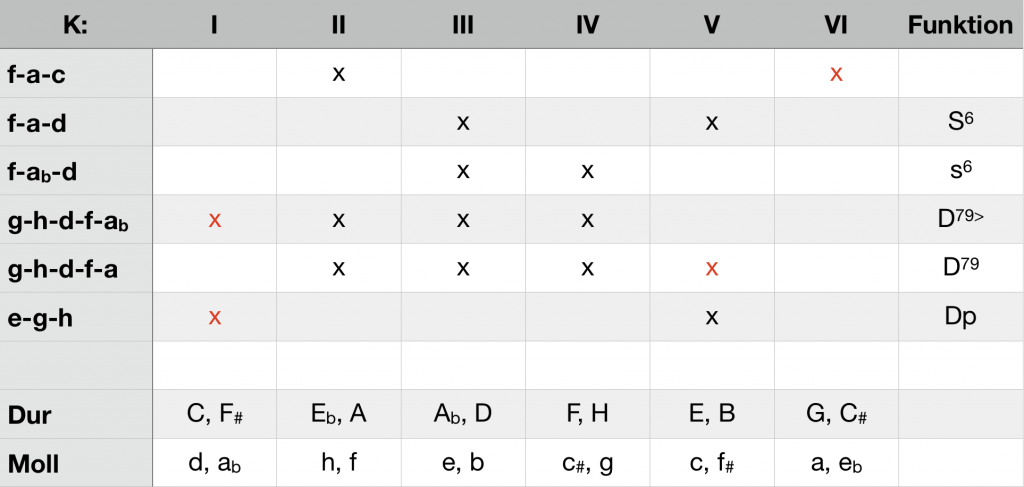
Leitungswirkung verschiedener Funktionsvertreter
Mit Hilfe der ci-Analyse lassen sich die zahlreichen harmonischen Enigma der reifen Klassik, der Romantik und des Impressionismus auf wenige Grundsätze zurückführen. Zentrales Movens der Weiterentwicklung der Harmoniesprache im 19. Jahrhundert ist die Relativierung der tonalen Eindeutigkeit der Klassik. Dies geschieht primär, indem die Ausrichtung auf eine komplementäre Struktur und die Einschränkung auf den Tonvorrat einer Zieltonart entkoppelt werden. Aus der Perspektive der Komplementarität sind die hierfür eingesetzten Mittel überraschend einfach:
- Ein Klang und dessen Tritonustransposition generieren identische Ausschlüsse, sind hinsichtlich der Ausrichtung auf eine K-Struktur wirkungsgleich. Dies wird gerne genutzt, um einen Funktionsklang durch besagte Transposition zu ersetzen. Welche Irritationen diese simple Maßnahme auslösen kann zeigen bereits die mannigfachen Deutungsversuche des Tristan-Akkords. Der Tonvorrat (f h d# g#) des Eingangsklangs im Vorspiel zu Richard Wagners Oper Tristan entspricht der Tritonustransposition eines d-Moll-Dreiklangs mit sixte ajoutée (d f a h). Zusammen mit dem nachfolgenden E-Dur-Septakkord ergibt sich zu Beginn des Tristan-Vorspiels eine Einschränkung auf die Strukturen K II (A-Dur) und K VI (a-Moll). Infolge der Aussparung des Lösungsklangs fehlt die konkrete Entscheidung; gleichwohl erfolgt eine rigide und präzise benennbare Einengung des Möglichkeitsraums. Hugo Wolf arbeitet gerne mit der Tritonustransposition dominantischer Klänge, notiert beispielsweise anstelle von G7 => C die Harmoniefolge Cis7 => C. Die Ersetzung des Quintfalls durch ein chromatisches Absinken in den Lösungsklang wird durch die Identität der von G7 und Cis7 generierten Ausschlüsse ermöglicht.
- Die von einem Septakkord generierten Ausschlüsse ergeben sich aus der Interaktion von dessen Quinte mit den anderen Klangbestandteilen. Beim Klang c-e-g-b sind dies die Komplementärintervalle c-g, e-g und g-b. Da die anderen drei Töne untereinander keine Komplemente ausbilden, wird eine Septakkord durch die Herausnahme der Quinte tonal entkernt. Die Reminiszenz an den klassischen Dominantseptakkord bei faktischer Atonalität ist ein u.a. von Robert Schumann genutztes Stilmittel und findet seine Fortsetzung im Impressionismus.
- Claude Debussy nutzt den Umstand, dass pentatonische Felder tonal ungerichtet anmuten, vermittels der in ihnen vorhandenen Komplementärintervalle jedoch den tonalen Möglichkeitsraum einschränken. Er entwickelt beispielsweise die tonale Progression konventionell bis zur Einengung des Möglichkeitsraums auf zwei K-Strukturen. Beim anschließenden Durchqueren eines pentatonischen Feldes wird eine dieser Strukturen ausgeschlossen. Die Integration des pentatonischen Feldes in eine recht weitgehend konventionelle harmonische Progression evoziert dann die charakteristische Wirkung des schwerelosen Schwebens in den Lösungsklang. (Vgl. Stegemann, 2013, p. 118ff)
In der nachstehenden Tabelle wird die Identität der Exklusionen bei der Ersetzung der Mollsubdominante mit sixte ajoutée durch eine Tritonustransposition in den Takten 2-3 des Tristanvorspiels (d-f-a-h ersetzt durch g# h d# e#, notiert als f-h-d#– g#), bei der Ersetzung eines D7 durch eine Tritonustransposition (c# e# g# h statt g-h-d-f), sowie die tonale Entkernung des Septakkords durch Herausnahme seiner Quint veranschaulicht. Tonale Pfade sind blau markiert.
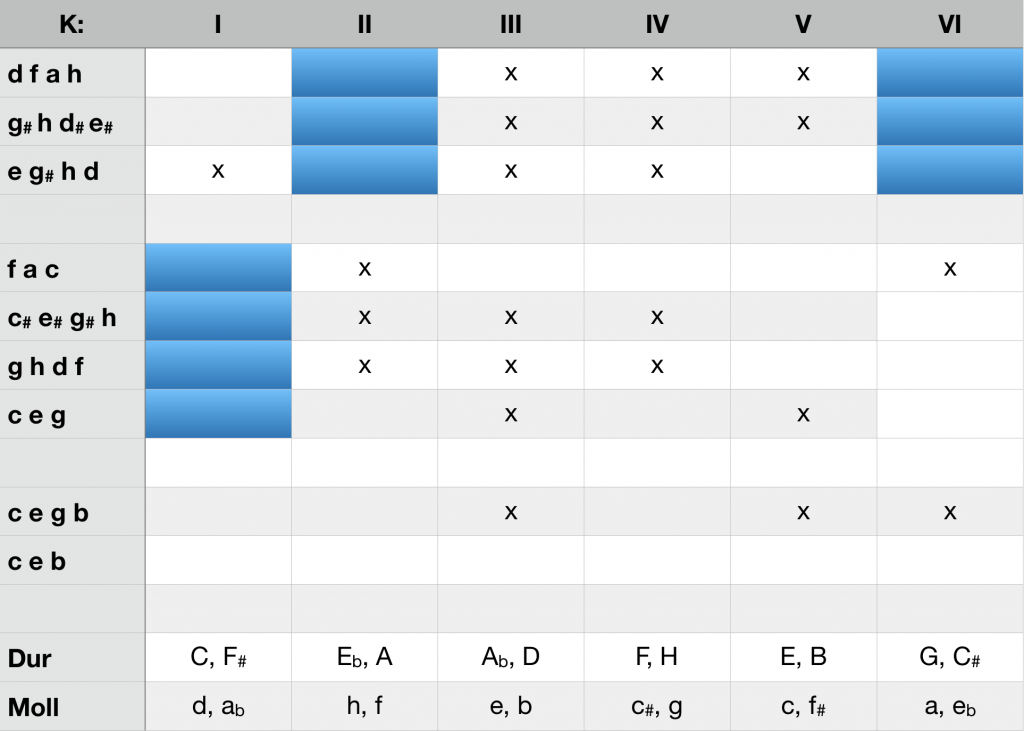
K-Identität der Tritonustransposition, tonale Entkernung des D7
Die Komponisten des 19. Jahrhunderts experimentieren ausgiebig mit der Möglichkeit, tonale Ziele zu verunklaren oder zeitweilig zu suspendieren. Gleichwohl bleibt Tonalität die Regel respektive der Bezugsrahmen, bleiben tonal irrelevante Klänge und atonale Klangfolgen die in einen tonalen Kontext eingebetteten Ausnahmen. Bei Arnold Schönberg ist die Situation invers. Sinn entbindet sich bei ihm oft aus der Beziehung sparsam gesetzter tonaler Ereigniszonen zum atonalen Kontext. Aus dem Vorhandensein dieser tonalen Abschnitte ergibt sich im Interesse einer soliden Deutung die Notwendigkeit, diese zu identifizieren. Die technische Basis zur Generierung tonaler Zonen im Zwölftonkontext verschafft sich Schönberg durch die Verwendung komplementärer Reihen: Nach der Setzung einer K-Achse im chromatischen Total wird zu jedem Ton x im 1. Hexachord einer Reihe dessen Komplement K(x) an beliebiger Stelle im 2. Hexachord gesetzt. Solange beide Hexachorde zeitlich getrennt bleiben ist es unmöglich, ci der zugrundeliegenden K-Struktur zu generieren. Das Tor zum Komponieren eines tonalen Abschnitts steht dann offen. Näheres hierzu findet sich im Tutorial Schönberg.

Für die Analyse eines Dreiklangs müssen drei Intervallkombinationen durchgeprüft werden, bei einem Fünfklang zehn. Hernach müssen die durch ci ausgeschlossenen K-Strukturen akkurat in einer Tabelle eingetragen werden. Bereits während der Erarbeitung der Beispielanalysen für die Theorie der Tonalität /Theory of Tonality erwies sich der damit verbundene Zeitaufwand als eminentes Hindernis. Die durch die Publikation der Theorie angeregte ci-App nimmt uns diese Arbeit ab. In der ci-App werden die Töne eines Klangs über eine virtuelle Tastatur eingegeben, Auswertung und Tabelleneintrag übernimmt die App. Der Zeitaufwand für das Erfassen der ci reduziert sich um deutlich über 90%. Die Tabellen lassen sich exportieren. Musiker und Musikwissenschaftler können sich daher bald auf die Interpretation der Ergebnisse konzentrieren. Die aufeinander aufbauenden Arbeitsschritte werden im App-Tutorial erklärt.