Guide
This post is also available in:
 Deutsch (German)
Deutsch (German)
In order to specify a content, music uses a number of means like a language: intonation, rhythm, modulations of volume and pitch. Its distinguished feature is the development of tone ordering systems. The alloy of melodic and harmonic ordering criteria proved to be particularly effective. In Europe, this development culminated in the major-minor tonality and favored the analytical privileging of harmonics. In order to make harmonic developments comprehensible, two empirically based models have been developed: the theory of the degrees and the functional theory. The rules of these models determined the understanding of tonal developments.
The primacy of major-minor tonality, together with the theory derived from it, limited an examination of tonal processes in the marginal areas or beyond the boundaries of this system. The harmonic-tonal innovations, especially from the beginning of the 19th century onwards, could therefore no longer be adequately grasped; tonal processes outside the system could not be explained anyway. Arnold Schönberg, in his Theory of Harmony, consequently called for a rethinking of the rules of the major-minor system and the fundamental laws of the phenomenon of tonality. But considering the dynamic evolution and diversity of Western music, musicology had long since moved away from the discussion of fundamental questions and concentrated on the development of analytical procedures deriving from the examination of concrete compositions. The rise of musicology from the 18th century onwards is based on this consideration of existing masterpieces. Schönberg’s postulate of an abstract regularity across all systems, prima facie pointing back to a past that had been overcome, therefore remained without any significant resonance.
It was Schönberg himself who finally identified a hidden symmetry as fundamental to tonal-harmonic processes, used it as the backbone of his complementary series and actually activated the immanent tonal option when needed. He documented his knowledge by means of his Suite for Piano op. 25, composed between 1921 and 1923, whose series is on the one hand complementary and thus conform to the basic tonal symmetry. At the same time, the series can be divided into three segments that are symmetrical to the axis that is perpendicular to the axis of symmetry which is constitutive for harmonic tonality in the torus of thirds. The last of these segments is the retrograde of the prominent tone sequence BACH. In 1921, Schönberg allowed himself a hint vis-à-vis his student Josef Rufer: “I have made a discovery which will secure the predominance of German music for the next hundred years.“ Since a discovery denotes something that already exists but has not been known until now, he apparently aimed at a matter of great importance that went beyond the development of the twelve-tone technique, but which is related to it because of its temporal coincidence. Indeed, the transfer of the tonality symmetry K from major-minor tonality to his own, henceforth complementary serial technique leads to the fascinating perspective of a suspension of the triadic aesthetic without abandoning tonality.
While the technique of composing with complementary series was adopted among others by Schönberg’s students Alban Berg and Anton Webern, there is no indication that an explanation of the tonal implication of the underlying symmetry was provided by its inventor. Schönberg restricts to general remarks on the tonality of a twelve-tone series and a rejection of the analytical methods established soon. As a result of this reluctance, the opportunity to place the empirically based analysis of harmonic processes on a more solid foundation as early as the 1920s remained unused. Respective demands in Schönberg’s extensive Harmonielehre did not initiate the development of adequate analytical procedures. A mandatory exploration of tonal orientation, for example in the compositions of the Romantic period, Impressionism and, in part, Dodecaphony, remained beyond reach until further notice. Schönberg’s discretion had far-reaching consequences for the examination of his oeuvre and its effect on the history of composition. In secondary literature, the structure-forming function of complementary series in atonal compositions is always appreciated without knowledge of the immanent tonal option. In fact, Schönberg occasionally activated that option, whereby the respective content is always reinforced by the coincidence of tonal development and form.
The existence of tonality symmetry K was first documented in 2003. This was followed in 2007 by the evidence that not only complementary series but also the classical cadence harmonics can be derived from this symmetry in every detail. In 2013 an analytical procedure derived from K – the ci-analysis – was presented, with the help of which tonal processes in compositions of Romanticism, Impressionism and Schönberg’s dodecaphony can be explored in detail. However, the examination of K and the integration of the results into the scientific discourse proved to be a lengthy process. This is due in no small part to the abstractness and novelty of the object. In an empirically determined subject like musicology, the adequate fundamentals must first be drawn up. A further hurdle arises from the fact that the results achieved by working with symmetry K are partially in contrast to doctrines that have been wrongly elevated to the rank of certainties over the decades, and actually dominate the composition-historical discourse. The fact that the 19th century, supposedly marked by the decay of tonal structures, developed strategies for a more subtle control of the tonal progression seems to take as much getting used to as the suggestion that Schönberg should not be one-sidedly appreciated as the father of atonality, but at the same time to acknowledge his contribution to integrate the tonal achievements of the 19th century into the development of a new system of tonal order.
Another hurdle is the time-consuming complexity of a ci-analysis without support. Extracting and tabulating complementary intervals needs patience and does not forgive any oversight. The development of an app that automates this process to a large extent has provided relief. The ci homepage and the present guide aim to further simplify access to this new analytical method and to facilitate the application-oriented transfer of analytical competence. An important step in this process is the emancipation from the limitations of habitual perspectives, the acquisition of a new point of view. A detailed tutorial then shows how to use the app to analyze a composition harmoniously and tonally and interpret the results, which are automatically documented in tables. Sample analyses then demonstrate which extended insights result from the application of the procedure depending on the respective epoch. While with regard to classical concepts, a deeper understanding of the known rules emerges, the analysis of especially romantic and impressionistic compositions and Schönberg’s dodecaphony leads to detailed new insights. Instead of describing a harmonic situation as, for example, vague or even atonal, the exact naming of the tonal options available as a result of a harmonic progression is now established. While an elimination of tonal perspective has so far been described as free-tonal or atonal in the same way as a extensive openness, ci-analysis detects such constellations as contradictory and thus allows a more precise definition of the possible intention or content.
The major-minor tonality, its evolution in the 19th century, as well as Arnold Schönberg’s twelve-tone technique can be derived from the hidden symmetry K. By evaluating the complementary intervals generated by K, tonal processes can therefore be detected in detail for the first time across the boundaries of different tonal systems. Furthermore, tonal border areas can be made accessible for analysis. Thanks to a specially developed analysis app, the method can be used by anyone interested.
Classical music obtains its vitality among others from the moving towards different tonal targets within a composition. The functional analysis is a successful instrument to illustrate such a development and to give hints with regard to the respective meaning of the content. Its application, of course, presupposes the primacy of the circle of fifths and the derivability of harmony from triads. The emancipation from this model intensified from the beginning of the 19th century. Various mutually stimulating tendencies can be observed:
- The search for substitutes for a function with constant orientation to a triadic basis
- The design of tonal progression with alternative chords
- The design of sections without clear tonal orientation
- The design of actual atonality
Since functional theory cannot grasp these developments in detail, the 19th century is described grosso modo as a time of tonal dissolution, with a supposedly logical progression to atonality in the 20th century. The tonality analysis with complementary intervals (from now on ci-analysis; ci = complementary interval) provides much more differentiated results. By visualizing the so called tonal paths, the tonal enigmas of the 19th century can be deciphered. Furthermore it can be proved that Arnold Schönberg used the complementarity of series to implant a tonal option, and that he activated it when desired.
Those who equate dodecaphony with atonality and derive compositional history from this premise will hardly recognize the tonal innovation in Schönberg’s compositional technique. In addition, the examination of a new analytical instrument requires more effort than the easy and arbitrary application of the labels tonal and atonal, which has become a habit. The amount of effort required is determined by the respective goal. For musicologists without a theoretical focus and for performing musicians, however, the effort to decipher advanced tonal structures must be kept within limits. This guide is particularly devoted to these musicians and musicologists: a practice-oriented approach provides the requirements for quickly analyzing interesting harmonic sections or even entire compositions. The resulting evidence of the tonal disposition can than serve as a basis for exegesis or one’s own interpretation. The theoretical basis of ci-analysis is therefore treated as concise as possible; it can be consolidated and deepened by studying the Theorie der Tonalität/Theory of Tonality (2013). Thanks to an analysis app developed by smartmobilesolutions, the detection and evaluation of complementary intervals is largely automated, thus radically reducing the time required. This makes ci-analysis applicable for every musician and musicologist without much effort. A step-by-step guide for working with the app makes access even easier.
The most important messages of music are not to be found on its surface. The actual concern of ci-analysis is therefore an aesthetic one: by bringing sublime harmonic constellations into consciousness, suggestions are made for deeper examination, for even more precise listening and presentation, for questioning the content. Relevant sample analyses will show which perspectives can arise here.
The inconsistent definition and imprecise use of the terms tonality and atonality is the result of a lack of analytical innovation. The scientific aporia prevents an appropriate examination of the phenomenon, that music is, across various tonal systems, frequently oriented to reference tones.
The use of the terms tonality and atonality is not secured by a authoritative definition. Predominantly, the major-minor tonality and the cadence harmony derived from it serve as a reference point for terminological orientation. Based on their method of tonal consolidation, no criteria can be designated to make a reliable distinction from the postulated atonality. The dichotomy tonal/atonal is thus potentially misleading due to the semantically incorrect use of the Alpha privativum: compositional practice is characterized by a continuum of tonal intensities or structures rather than by a tonal dichotomy.
The described terminological carelessness is an expression of a deeper embarrassment. The traditional tools of tonality analysis are derived from the robust major-minor tonality and are therefore only partially suitable to detect or interpret fragile structures. The harmonic innovations of the Late Classical, Romantic and Impressionist periods can therefore only be rudimentary understood by means of functional theory or the theory of the degrees. The resulting gaps are rather skipped than closed by contestable interpretations and characterizations. Where the area of this descriptively explored tonal vagueness ends and changes into atonality is at the discretion of the respective author, due to the absence of delimiting criteria. The ex cathedra statements of atonality that have become commonplace should therefore be considered critically. They conceal the scientific aporia and de facto prevent the heuristic gain suggested by the use of the term.
The unreflective handling of the term pair tonality/atonality is so firmly anchored in scientific discourse that the necessity of a critical examination is hardly recognized. This is particularly worrying with regard to the oeuvre of Arnold Schönberg and its effect on the history of composition. Throughout his life Schönberg was confronted with the challenge that a further development of complexity and expression would make what he called the comprehensibility (Fasslichkeit) of a composition more difficult. Since he wanted to be understood despite the high standards of composition he set for himself, he by no means abandoned the eminently important means of tonality for structure and orientation with the transition to dodecaphony. He rather integrated the tonal option by using complementary series and activated it occasionally: complementarity is based on the hidden symmetry K, from which major-minor tonality can be derived in detail. In fact, Schönberg made multiple use of the possibility to create tonal sections, the respective meaning of each can be explained by its formal and substantive relevance in a structure dominated by non-tonal parts.
Schönberg was a pioneer of non-tonal composing and at the same time involved in the further development of an expanded tonality based on the major-minor system. He thus rejected the simplifying dichotomy of tonal/atonal. A classification by means of an ostensible opposition is hardly appropriate to be the object of scientific and aesthetic debate. It makes more sense to comprehend tonal structures even beyond the major-minor system and to distinguish them from actual non-tonal structures. This requires both the development of suitable analytical instruments and aesthetic awareness. By stating alleged atonality, one merely relieves oneself of the effort and responsibility to appreciate the scientific and artistic perspectives provided by the tonal expansions of the 19th and 20th centuries.
Tonality is not subject of a particular system, but the usual rules for its analysis are unilaterally derived from major-minor tonality. In order to be able to study the phenomenon beyond system boundaries, knowledge of empirically obtained rules is necessary, as well as knowledge of fundamental laws. Their exploration is not favored by the strong empirical orientation of musicology since the 18th century.
The rules of classical harmony derive from the existence of keys and triads. Consequently, the knowledge about the expansion of the tonal horizon becomes blurred and finally impossible with increasing distance from those basic patterns. Arnold Schönberg criticized this in his Harmonielehre, first published in 1911, and called for a system based on natural laws. At the same time, he stated that he had not (yet) found such principles himself. A good century later, the discipline is still struggling with the challenge he has named: in tonally advanced compositions, the analytical examination of the increasing subtlety and fragility of the tonal disposition is becoming more and more important in principle, while its presentation using traditional methods seems increasingly questionable.
The attitude of musicology towards this challenge is peculiar. Although a binding definition of the term tonality did not exist (and still does not exist), atonality was set as the opposite without naming a delimiting criterion. Since many tone phenomena could not be assigned to either of the two terms with certainty, further terms such as floating or suspended tonality were created for the area between the opposites tonality and atonality. In the concrete application of this terminology, one searches in vain for valid reasons: The label atonality is primarily used for compositions that cannot be explored with traditional analytical methods; dodecaphonic and dissonant compositions are preferred objects of such classification. Moreover, the dichotomy established by the Alpha privativum implies: tertium non datur, does actually not allow the establishment of an intermediate tonal area. Instead of contributing to the understanding of tonal developments, the restriction of the discourse to the dichotomy tonal/atonal avoids a discussion and prevents knowledge.
When looking out for reasons to explain the absence of analytical innovations, a glance to the history of music theory is advisable. In antiquity, together with arithmetic, geometry and astronomy, music was assigned to the mathematically oriented quadrivium. The concentration on fundamental questions continued in the Middle Ages. This limited the possibilities of grasping and reflecting on the developments and upheavals in Western music history. A paradigm shift towards the examination of concrete compositions (Arbeit am Werk) put music theory back on the road to success. Consequently, the focus of the debate shifted from the fundamental and abstract issues to the empirical ones. The rules now derived from concrete compositions and then applied to these in turn have relevance within a tonal system or within a limited historical period, but no general validity.
The striving for tonal orientation manifests itself in many respects across epochs, systems and cultural boundaries. In church modes, the structure of the melody and the definition of the ambitus determine the allocation of tonal meaning, while the material remains the same. The melodic foundation of tonality is supplemented in the historical course by a harmonic one. The vanishing point of this development is the triad-based harmony of classical music. From here, the 19th century progressed to the point where it was often no longer possible to derive complex chords from triads. Afterwards, Arnold Schönberg attempted to implant a tonal option in some of his complementary series and made use of it. The methods of analysis derived from major-minor tonality are not able to adequately grasp and evaluate tonal processes in the margin areas or beyond the limits of the underlying system. For their understanding, the knowledge of the scientific laws, which overcome, according to Schönberg, the limits of tonal systems, is indispensable. However, an awareness of the necessity to develop correspondingly abstract analytical skills is hardly pronounced in musicology, which is focused on the successful model of empirical „Arbeit am Werk“. Thus, the actual examination of the phenomenon of tonality has been replaced by the narrative of its dissolution in the 19th century, which was allegedly completed in the 20th century by Arnold Schönberg’s transition to atonality. Schönberg vehemently argued against the equation of atonality and dodecaphony, but apparently did not find himself willing to inform even his outstanding students about the insights he had gained. He didn’t inform anybody about his knowledge of controlling harmonic-tonal processes in the twelve-tone space. Apologists and scientists have therefore never dealt with Schönberg’s technique of relating atonality and systemically secured tonality in serial compositions. The one-sided reception of his oeuvre, directed toward the atonal perspective, imposed a further detour to musicology, music theory and the history of composition.
Chords shape the tonal space of possibilities. While the achievement of concrete tonal goals loses importance aesthetically and with regard to the content, the examination of the spatial structure generated by the chords respectively the tonal directions of movement become relevant for the comprehension.
The conventional tools for analyzing tonal structures are an expression of a specific aesthetic. It is based on the idea of a harmonic balance, which is occasionally – especially through dissonances – violently irritated, but not suspended. In classical music, the tonic is the symbol and tonal goal of this ultimately maintained balance. It is not without reason that the relevant examination of chord sequences is called theory of harmony. The idea of harmonic proportions or relationships had a formative influence on architecture, art, the humanities and the natural sciences for multiple epochs. This is also valid for its negation, when a loss of balance is perceived and shaped. In music, the romantic 19th century in particular benefits from this possibility. There, lovesickness is illustrated by the loss of the tonal center. And a sudden switching to a distant key often illustrates alienation or madness. Musicology traditionally and persistently seeks to interpret the results with the help of two complementary antonyms: These are the pairs of the opposites consonance/dissonance and tonality/atonality.
By stating the emancipation of dissonance, Arnold Schönberg described a development at the end of which tonal processes can no longer be interpreted from the interrelation of opposed classes of chords. To the extent that dissonances were perceived as independent phenomena, the dichotomous classification of consonances and dissonances lost its relevance.
The introduction of the term atonality was problematic from the beginning. Tonality is not a term secured by a clearly defined definition, which is why the dichotomy postulated by the alpha privativum is not sufficient for classification. The classification of compositions as tonal or atonal is therefore often arbitrary and seldom leads to a gain in knowledge. In practice, the formal dichotomy tonal/atonal is treated as a polarity anyway. In fact, tonality and atonality appear as vanishing points of a nuanced tonal space. The usual characterizations of the processes perceived in this space, for example as “floating” or “vagrant” (Schönberg), do not allow, in their vagueness, a detailed statement with regard to expression or meaning.
It is necessary to reflect on the altered aesthetic situation and to consider the consequences for an analytical examination. In advanced harmonic structures, potential tonal goals are means of design, but no longer necessarily a vanishing point of development. Movements in the tonal space of possibilities are no longer subject to any judgement with regard to their orientation. The narrowing of this space due to the discontinuation of tonal options can easily be stopped and reversed before a tonal goal is reached. Developments can be interrupted or delayed by the introduction of tonal undirected sections. A dichotomous classification of such heterogeneous processes is obviously not appropriate. Also, an analysis with the help of the functional theory or the theory of the degrees derived from scales and triads soon reaches its limits, because the privileging of a certain selection of pitches or certain chords in tonally advanced compositions cannot be assumed.
Since the achieving of a tonal goal in an advanced composition is only an option and not a prerequisite, such a goal can no longer be the exclusive reference point of an analysis appropriate to the subject. This analysis must grasp the modifications of the space of possibilities and therefore proceed with reversed auspices. No goal is postulated, but rather it is first determined which tonal goals are rendered obsolete by a chord or a sequence of chords: The synopsis of the respective restrictions then illustrates the current structure of the space of possibilities. As will be demonstrated, complementary intervals precisely indicate the omission of tonal options. They are therefore particularly suitable for capturing more complex tonal processes and making them accessible to an analysis. It is irrelevant whether a chord is consonant or dissonant according to conventional classification or if it can be derived from a triad. The ci-analysis based on the acquisition of complementary intervals makes visible which tonal paths are shaped by chord sequences. It is therefore predestined for the examination of complex harmonic processes.
Harmonic tonality is the result of an appropriate sequence of chords. Throughout this tonal progression, potential targets are successively eliminated. At the end of such a development there results often, but not necessarily, a binding orientation towards a tonal center.
Harmonic tonality is the result of a purposeful and planned sequence of chords. The standard cadence (T S D T) is the paradigm of such a process, here directed towards tonal centering, while functional theory is the customized means of its analysis and representation. A cadence successively reduces the number of tonal options until only one goal remains. For this purpose it can be limited to the pitch classes of the scale assigned to the target. Especially from the 19th century onwards, compositional practice emancipated from this model in two respects. On the one hand, in the search for tonal orientation, pitch classes foreign to the scale are applied increasingly; in addition, tonal alternatives which cannot be completely derived from triad models. On the other hand, contents and expressions developed which cannot be represented in the seclusion of a tonal world focused on the tonic: Openness, uncertainty, forlornness or detachment; breaks, turnarounds, crashes, craziness and reverie.
In addition to the orientation towards a tonal target, other options of tonal design become relevant. For example, at the end of a harmonic development, two potential tonal targets may remain; frequent changes of perspective without final alignment to a target or abrupt changes of the tonal frame of reference may widen the space of possibilities up to a quasi disoriented openness; condensed chords may destroy any perspective.
In order to find a starting point to decipher tonal advanced models, it is helpful to first consider the possibilities and limitations of conventional functional analysis. This analysis concentrates on the model of an ultimate orientation of the tonal progression to a tonal center. In doing so, it succeeds in establishing a hierarchy of tonal side-stages, which are often meaningful with regard to the content. Furthermore, the pooling of different chords into functional groups provides clarity. However, the assignment of a function largely ignores the qualities of a chord apart of this function. A functional designation indicates, for example, that a subdominant is set in minor or major, or that a fifth is supplemented or replaced by a sixth. It does not, however, make any statement about how the subordinate space of possibilities is modified by a particular function representative. In fact, the intrinsic qualities of a functional representative are already of significance in classical music: Thus, prior to a modulation to the dominant, the replacement of the standard subdominant by an s6 respectively S6 is appropriate (opening of the dominants space), whereas a sixth ajoutée is not. The empirically established privileging of a chord in a specific context can give an indication of the subordinate space of possibilities. However, it is not able to specify its structure and to justify it in detail. This becomes definitely problematic when tonally relevant chords can no longer be functionally assigned, or when given assignment possibilities find no equivalent in aesthetic experience.
In order to find an access, an analytical antagonist is therefore required. A method that initially ignores the question of the hypothetic target, but determines which goals can no longer be reached.
Harmonically tonal processes in the twelve-tone space can be deduced across systems from the hidden symmetry K. That K is the backbone of Schönberg’s complementary twelve-tone series as well as of major-minor tonality became apparent in the course of the discussion that followed its discovery. This led to the development of a method of tonality analysis through the detection and allocation of complementary intervals.
The history of ci-analysis began with the discovery that Arnold Schönberg used a hidden symmetry, henceforth labeled „K“, to generate his complementary series (Stegemann, 2003). K can be illustrated by placing a mirror axis at any point in the chromatic scale. In the following example, this axis is located between the pitch classes b and c, which, with regard to the mapping ratios, leads to identical results as an inserting between f and f#:
f# g g# a a# b | c c# d d# e f
In the concrete case the pitch class f is the symmetry partner of f#, e is the symmetry partner of g, or expressed mathematically: f = K(f#), e = K(g) … c = K(b). In a manifest symmetry, the symmetry partners are directly comprehensible (visible) related to each other. In the case of symmetry K, on the other hand, a pitch class x and its complement K(x) are separated from each other, e.g. by assigning them to different sets of pitch classes. In a complementary twelve-tone series, this separation is achieved by the fact that the settlement of a pitch class in the 1st hexachord causes the settlement of its complement in the 2nd hexachord. This can be easily understood, for example, when looking at the series of Schönberg’s Piano Concerto op. 42.

The K-axis of the row is situated between the pitch classes b and c (respectively f and f#). Complement of the 1st row tone (RT) eb is the 8th row tone g#, complement of the 2nd row tone b is the 9th row tone c#. d = K(a) (RT 10), f (RT 4) = K(f#) (RT 7), e (RT 5) = K (g) (RT 12) and c (RT 6) = K(b) (RT 11). The complements of the series tones 1 to 6 are thus all in the second hexachord. This is illustrated by coloring the pitch classes of the 1st hexachord in the chromatic scale. Each red colored tone is mapped by K on a non-colored one:
f# g g# a bb b | c c# d eb e f
This classification is valid in all complementary series, whereby the respective position of K in the chromatic scale must be determined.
By examining a row surface or playing the successive row tones, K cannot be located, especially since the pitch classes within a hexachord can be rearranged in any order without canceling the complementarity of a row. This absence of obvious symmetry is probably the reason why K remained undiscovered for so long. If K were merely the ordering principle for complementary series, such ignorance would not have any far-reaching consequences. During the study of the regularity of K, however, it was noticeable that Schönberg occasionally privileged the second pitch class to the left of the K-axis or its tritone transposition within a K-structure, thus creating a latent tonicality. In op. 42 the tonal privileged position concerns the pitch class b flat. This is also visible on the surface of the row in the form of the B-flat major triad shaped by the row tones 3-5. In the case of a composer who hardly ever left anything to chance, this stimulated further discussion. It initially led to the observation that even a classical standard cadence (T S D T), the core element of a completely different twelve-tone system, is K-compatible (Mazzola/Stegemann, 2007). Here, an explanation of what compatibility means in this context is needed first:
- Since identical mapping conditions are restored after six semitone shifts in the chromatic scale, six different K-structures can be generated by inserting K in that total.
- Only the interval classes minor second, minor third and fourth as well as their respective reverse intervals major seventh, major sixth and fifth are affected by complementarity. These are the intervals generated by an axis of symmetry between two notes of the chromatic total.
- In the exemplary major triad bb-d-f, the intervals bb-f and d-f are thus complementary in certain K-structures.
- For example, if the K-axis is placed between the pitch classes b and c (respectively f and f#), none of the intervals contained in the triads of B-flat major, E-flat major and F major (the tonic, subdominant and dominant of B-flat major) generates a complement in the resulting structure. In each of the other five K-structures, at least one of these intervals is complementary. Consequently, the B-flat major cadence can solely be shaped in the K-structure where the axis K is placed between the pitch classes b and c (f and f#, respectively). The key of B flat major can thus be assigned to this structure. Such an assignment possibility exists for each of the twelve major and twelve minor keys.
The comparative examination of cadential harmony with Schönberg’s serial technique referred to a fundamental importance of complementarity with regard to tonal orientation in the twelve-tone space. This made it possible for the first time to demonstrate a regularity of tonal stabilization through chord progressions that combines two different tonal systems:
A complementary interval excludes the tonal structure assigned to it as a place of tonal stabilization. K-structures can be successively excluded by a sequence of purposeful chords, until only one structure remains. This orientation towards a single K-structure is a prerequisite for tonal fixation and is not limited to a particular tonal system.
While dealing with the implications of complementarity, crucial issues concerning major-minor tonality are enlightened: its expansion especially in the 19th century, as well as the integration of the tonal option into Schönberg’s dodecaphony. A key is defined by its tonal material – the seven-degree scale – and the triads derived from it. Nevertheless, the five remaining pitch classes not inherent in the scale occasionally contribute to the the tonal development. On the one hand, this is done as expected to deliberately and effectively delay the tonal consolidation. At the same time, pitch classes that do not belong to the scale can also contribute to the consolidation, and with the expansion of tonality in the 19th century, entire chords from foreign cadence contexts are integrated into the tonal development. The supposed contradiction dissolves when one becomes aware that the complementary intervals used are responsible for the orientation towards a K-structure. The possible affiliation of the interval components to the pitch class-stock of the target key is irrelevant for this alignment. The pitch class-stock becomes relevant with the next step: Since each K-structure is the basis of two major and two minor keys (more details in the following chapter), the range of pitch classes must be narrowed down to confirm the target key. The fixing of a key is thus a process that can be divided into two parts:
- Step I: By generating appropriate complementary intervals, the alignment to a certain K-structure is confirmed.
- Step II: Alignment to one of the four keys of the selected K-structure is ensured by purposeful reducing the number of pitch classes.
In the interest of the swift determination of a key, classical harmonics alloys the two steps, combines the orientation towards the respective K-structure with a substantial limitation to the pitch class stock of the target key. The analysis methods derived from classical harmonics – functional theory and the theory of the degrees – require this alloy. The harmonic methods of the 19th century, on the other hand, often aim to delay the tonal decision or even refuse it. In order to achieve this, a sequence of the steps mentioned is necessary. Unfortunately, functional theory and the theory of the degrees are not suitable to capture and then interpret in isolation the part of a harmonic progression based on the first step. The eminent advantage of ci-analysis is based on making this part of the progression visible, precisely mapping the delimitation of the tonal space of possibilities through complementary intervals. As a result, numerous enigmas of the Romantic and Impressionist harmonic language dissolve: they can be explained by the narrowing of the tonal space of possibilities through complementary intervals (step I), without the tonal goal having already been indicated by an appropriate limitation of the pitch class set or the triadic material. This orientation towards the goal is only achieved – if at all – with the subsequent step II.
The examination of the regularities of a twelve-tone space structured by K updates the insights regarding the fundamental relevance of the triad. In the 19th century, it is possible to emancipate the harmonic progression within limits from the triad. Since four potential tonal targets still exist after alignment with one of the six K-structures, the binding force of the triad with regard to tonal confirmation nevertheless maintains its significance even in harmonically advanced compositions. Arnold Schönberg strives for further emancipation from the triad. His central idea of composing with twelve pitch classes that are only related to each other does not, however, find an unrestricted correspondence in his oeuvre. Since he deals almost exclusively with complementary series, of the 924 possible dichotomies for dividing the chromatic total into hexachords, only the twenty with complementary structure are available to him, of which he actually uses fifteen. Schönberg, like the Romantics and the Impressionists before him, is confronted with the challenge that every expansion in the tonal space of possibilities is combined with a decrease in comprehensibility. In fact, due to the concentration on complementarity, about 98% of the dichotomies remain unused: the expansion of the scope of possibilities is small in view of the claim Schönberg makes. And since there are four keys in each K-structure, there is still a tendency in Schönberg’s compositions to use dichotomies with tonal implication, in which the triadic components of the latent tonic converge in a hexachord. In the Piano Concerto op. 42, this triad is even exposed on the surface of the row in the form of the row notes 2 to 4. Thus, even in serial compositions, the triad remains the most effective means of affirming a tonal goal.
As will be shown later on, Schönberg uses his serial techniques, if required, purposeful to shape tonal sections or formal parts. Wherever he does so, his compositions obey to the laws of complementarity in the same way as major-minor tonal compositions did previously. The tonal paths that become visible through ci-analysis document this impressively.
Sources:
- Mazzola, Guerino & Stegemann, Benedikt: Hidden symmetries of classical tonality in Schönberg’s dodecaphonic compositions, in: Journal of Mathematics & Music, p. 37-51, Oxon, 2007
- Stegemann, Benedikt: Arnold Schönbergs musikalische Gedanken, Frankfurt, 2003
- Stegemann, Benedikt:Theorie der Tonalität / Theory of Tonality, Wilhelmshaven, 2013
Harmonic-tonal processes in the twelve-tone space can be revealed beyond system boundaries by detecting and assigning complementary intervals. Thanks to the development of a useful app, this time-consuming process has been radically simplified and accelerated. In order to understand the process, however, an examination of the fundamental regularity remains indispensable.
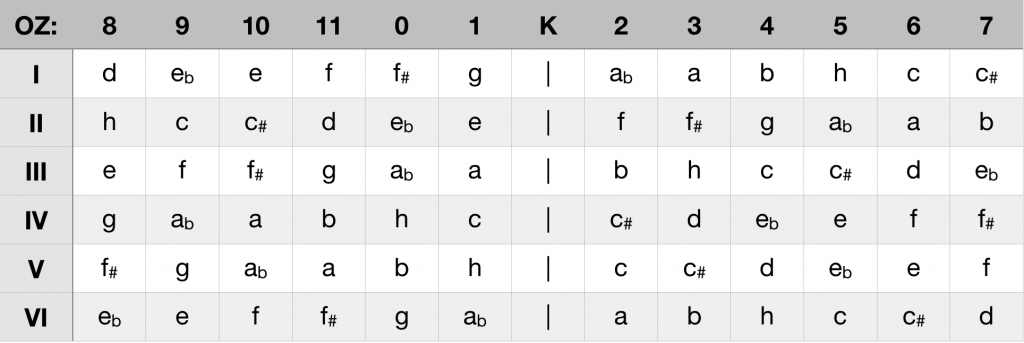
As mentioned in the previous chapter, six different K-structures are generated by the successive shifting of axis K within the chromatic scale. The basic property of K is the separation of the symmetry partners: The settlement of a tone x leads to the exclusion of its complementary symmetry partner K(x). The exclusion refers to a possible simultaneity, allows the appearance of x and K(x) in chronological succession. The mapping ratios of the six K-structures, now numbered from I to VI, are shown in the following table:
The mode of action of the ci-analysis can be illustrated by looking at the standard cadence of C major, for instance. The tonic triad c-e-g contains the complementary interval c-g from the K-structure III as well as the interval e-g from structure V. K III and K V are thus ruled out as a possible place of tonal consolidation, since the intervals mentioned are not permitted in these structures. The subdominant f-a-c contains the interval f-c from K VI and the interval a-c from K II, the dominant g-b-d contains the interval g-d from K II and the interval b-d from K IV. The standard cadence of C major thus generates complementary intervals in the K-structures II, III, IV, V and VI. Its tonal basis is K I. Keeping a K-structure (here K I, marked in blue) open in a harmonic progression is referred to in the following as the tonal path.
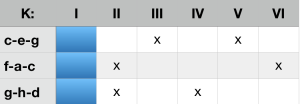
Tonal path of the C major standard cadence
The following table provides a survey which triad generates a complementary interval in a respective K-structure. A synopsis concerning the feasibility (+) or non-feasibility (-) of all major and minor triads in the six K-structures makes evident, that each cadence can be realized exclusively in one K-structure, and that each K-structure is the basis of two major and two minor keys. In K I these are the cadenzas of C major (red) and F-sharp major (blue), of D minor (red) and A-flat minor (blue):
Major triads
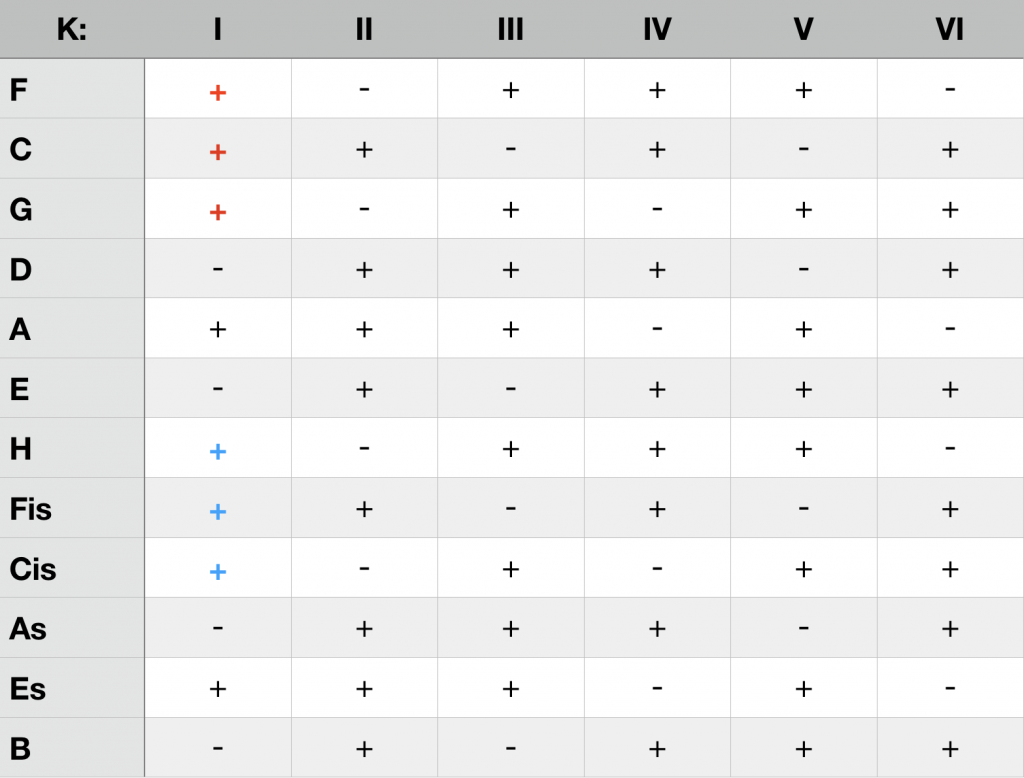
Minor triads
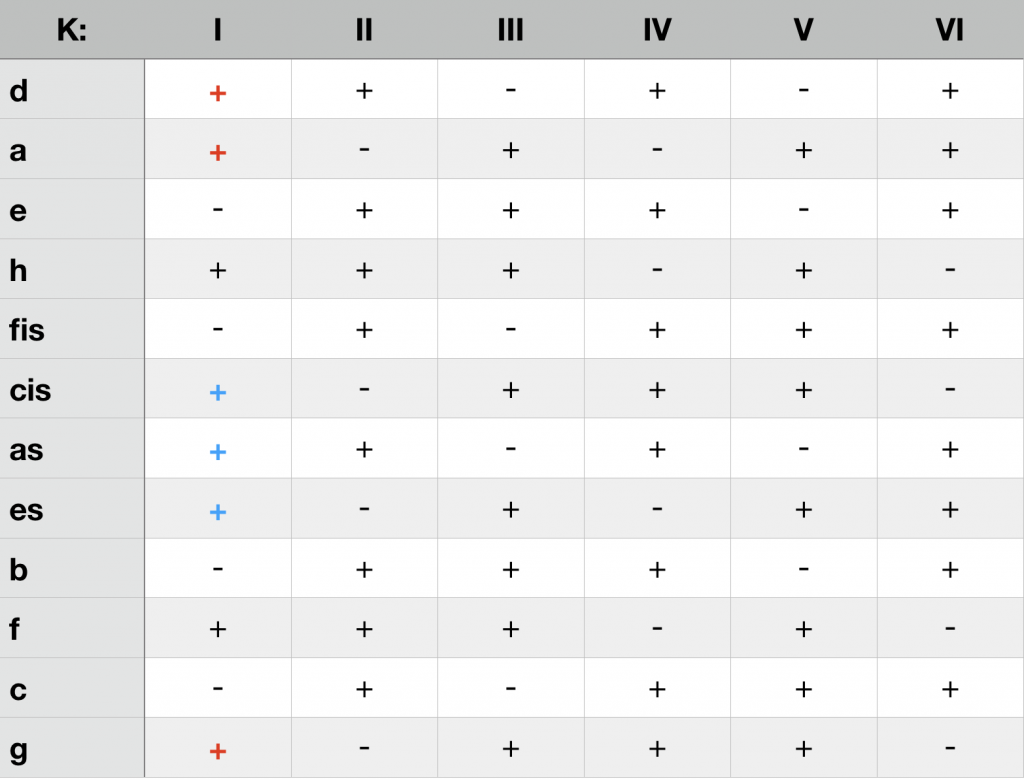
Using the triad tables, a K-structure can be assigned to each cadence and thus to each key. The following table provides a survey of the assignments as well as the intervals that are not allowed in the respective structure because they are complementary.
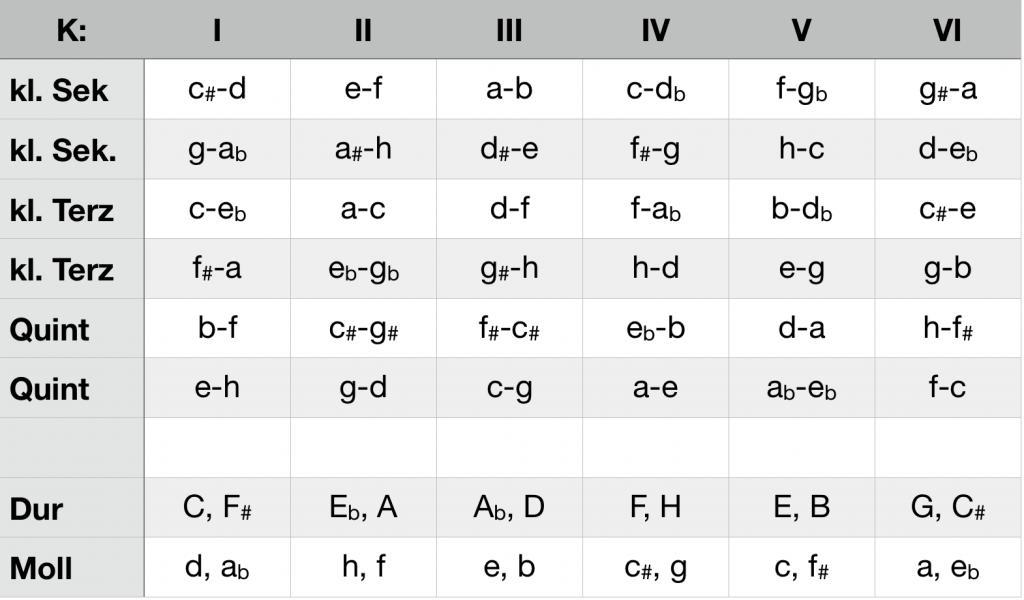
ci and keys of the six K-structures
In the harmonically advanced music of the 19th and 20th centuries, the tonal progression can partially no longer be derived from triads. However, it can be deduced by extracting the complementary intervals from the chords. Due to the assignment of the ci to a K-structure, their respective contribution to the modeling of the tonal space of possibilities can be elicited. The listing of the exclusions generated by the complementary intervals in tables provides a survey of the tonal progression. Since, for example, ten interval relationships have to be investigated and, if necessary, assigned for a five-tone chord, the effort is very high and prone to error. Working with the ci-App puts the analysis on a new basis, since after the input of the tones of a chord, the evaluation and the tabular preparation are automated. The actual procedure is the subject of a tutorial.
The core processes of classical harmonic can be well described with the functional theory tailored for this purpose. Nevertheless, ci-analysis deepens the understanding and provides information in detail. Below are some examples, some of which are explained in more detail in the Classic Tutorial:
- In the C major cadenza, only the interval f-c contained in the subdominant triad excludes the K-structure of the dominant (K VI). Therefore, K VI remains open when deciding on the function representatives S6, s6 or sn . Knowing the facts, the frequency of the occurrence of especially a S6 or s6 in the context of a modulation towards the dominant can be empirically examined.
- In the chord g-b-d-f-a the interval d-a prevents a tonal consolidation in K V, in g-h-d-f-ab the interval g-ab prevents a consolidation in K I. The addition of a major ninth to a dominant seventh chord thus negates the possibility of a following minor tonic, the addition of a minor ninth negates a major tonic. This steering function of major and minor ninth is diligently included in compositional practice.
- The function Dp generates a complementary interval in the K-structure of the tonic. In the case of C major, this is the interval e-b in K I. In fact, this function is not relevant for the consolidation of the tonic.
- The sixte ajoutée is labeled as the characteristic dissonance of the subdominant, the minor seventh as the one of the dominant. Notabene, a dissonance can only be characteristic if, in the K-structure of the tonic, it cannot be assigned equally to the dominant and to the subdominant. The sixte ajoutée is the only supplement to the basic triad that fulfills this requirement with regard to the subdominant, independent of the mode; in the case of the dominant, it is the minor seventh.
The following table gives a survey of the exclusions generated by different function representatives. The relevant one in the context discussed is marked in red.
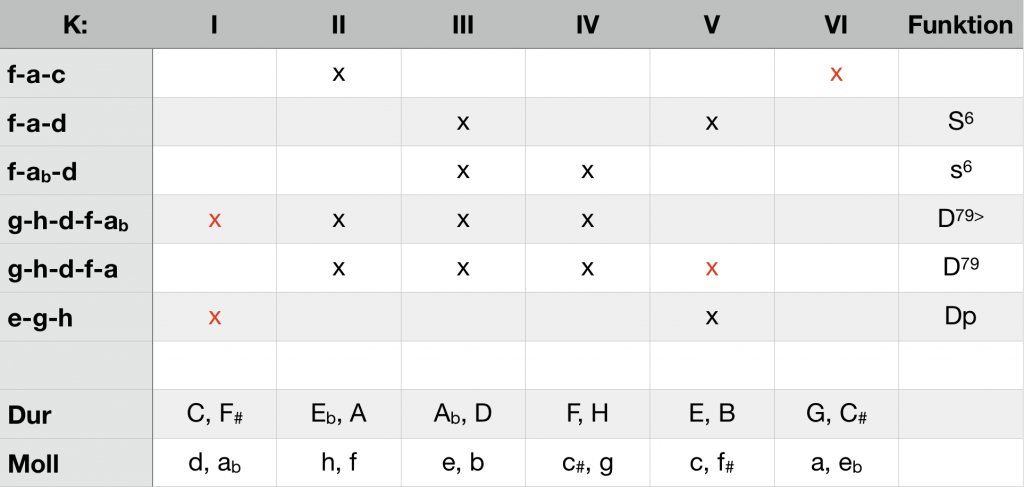
Steering effect of different function representatives
Assisted by ci-analysis, the numerous harmonic enigmas of the mature classical period, of romanticism and impressionism can be traced back to a few principles. The central motive for the further development of the harmonic language in the 19th century is the relativization of the tonal clarity of the classical period. This is done primarily by unraveling the orientation towards a complementary structure from the restriction to the tonal repertoire of a target key. From the perspective of complementarity, the means used for this are surprisingly simple:
- A chord and its tritone transposition generate identical exclusions, are equivalent with regard to the orientation towards a K-structure. This fact is often used to replace a functional chord by the aforementioned transposition. The irritations this simple measure can cause are already obvious when looking at the many attempts to interpret the Tristan chord. The tonal material (f b d# g#) of the initial chord in the prelude of Richard Wagner’s opera Tristan corresponds to the tritone transposition of a D minor triad with sixte ajoutée (d f a b). Together with the following E major seventh chord, the beginning of the Tristan prelude is restricted to the structures K II (A major) and K VI (A minor). As a consequence of the omission of the tonal target chord, the concrete decision is avoided; nevertheless, a rigid and precisely nameable restriction of the space of possibilities takes place. Hugo Wolf likes to deal with the tritone transposition of dominant chords, e.g. instead of G7=> C he notes C#7 => C. The replacement of the descending fifth by a chromatic sliding to the tonal goal is made possible by the identity of the exclusions equally generated by G7 and C#7.
- The exclusions generated by a seventh chord result from the interaction of its fifth with the other tones. For the chord c-e-g-bb, these are the complementary intervals c-g, e-g and g-bb. Since the other three tones do not form complements with each other, a seventh chord is tonally eroded by removing the fifth. The reminiscence of the classical dominant seventh chord with factual atonality is a stylistic device used by Robert Schumann and others and is proceeded further in Impressionism.
- Claude Debussy makes use of the fact that pentatonic segments seem to be tonally undirected. By means of the complementary intervals they contain, they nonetheless restrict the tonal space of possibilities. For instance, Debussy shapes the tonal development in a conventional way until the space of possibilities is narrowed to two K-structures. When subsequently traversing a pentatonic segment, one of these structures is excluded. The integration of the pentatonic segment into a largely conventional harmonic progression then evokes the characteristic effect of weightless floating to the tonal goal. (Cf. Stegemann, 2013, p. 118ff)
The table below illustrates the identity of the exclusions when replacing the minor subdominant with a sixte ajoutée by its tritone transposition in bars 2-3 of the Tristan prelude (d-f-a-b replaced by g# b d# e#, notated as f-b-d#– g#). The situation is analogue, when we replace a D7 by its tritone transposition (c#-e#-g#-b instead of g-b-d-f. The ultimate example illustrates the tonal erosion of the seventh chord when removing its fifth. Tonal paths are marked blue.
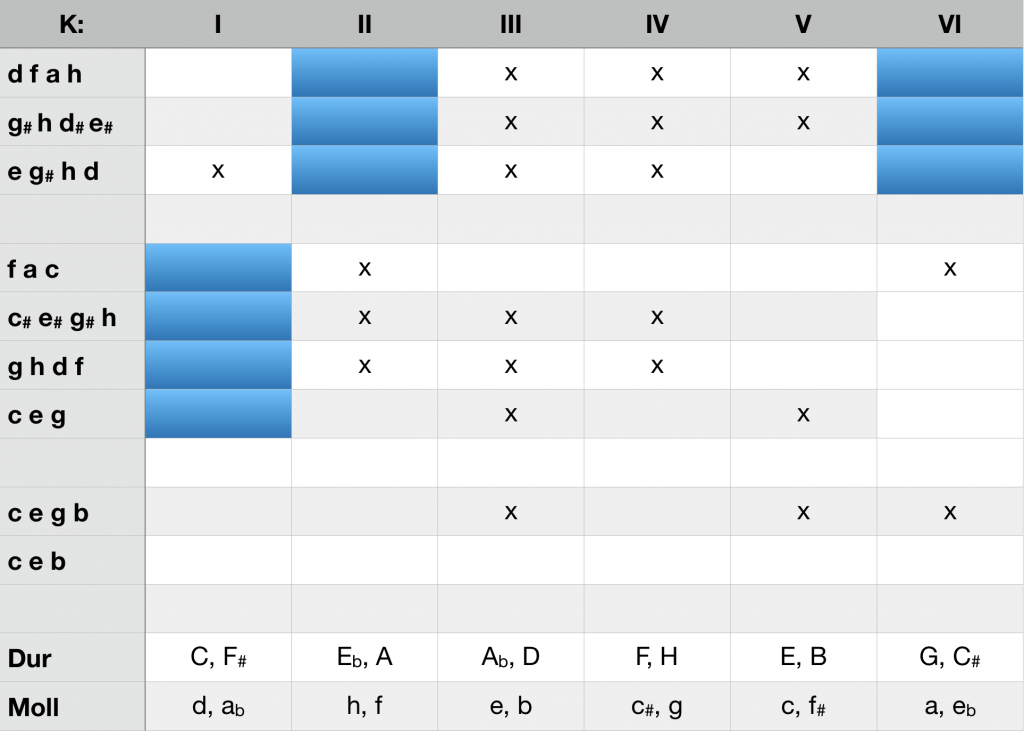
K-identity of the tritone transposition, tonal erosion of the D7
The composers of the 19th century experimented extensively with the possibility of obscuring or temporarily suspending tonal goals. Nevertheless, tonality remains the rule or the frame of reference. Tonal irrelevant chords and atonal chord sequences remain the exceptions embedded in a tonal context. With regard to Arnold Schönberg the situation is inverse. In his oeuvre, meaning often results from the relationship of sparingly outlined tonal zones to the atonal context. In the interest of a solid interpretation, the presence of these tonal sections makes it necessary to identify them. The technical basis for the creation of tonal zones in the twelve-tone context is provided by Schönberg through the use of complementary series: After placing a K-axis in the chromatic total, the complement K(x) of each note x in the 1st hexachord of a series is set at any position in the 2nd hexachord. As long as both hexachords remain separated, it is impossible to generate ci of the underlying K-structure. We are thus free to shape a tonal section. For more information, please check the tutorial concerning Schönberg.

For the analysis of a triad, three combinations of intervals must be checked, ten for a five-note-chord. Afterwards the K-structures excluded by ci must be accurately registered in a table. Already during the preparation of the example analyses for the Theory of Tonality, the time required for this proved to be a major obstacle. The ci-App, whose development was inspired by the publication of the Theory of Tonality, relieves us of this effort. In the ci-App, the tones of a chord are entered via a virtual keyboard. Evaluation and the registration in the table is done by the app. The time required to record and analyze the ci is reduced by well over 90%. The tables can be exported. Musicians and musicologists are then free to concentrate on the interpretation of the results. The app tutorial explains the consecutive operations.