Glossary
This post is also available in:
 Deutsch (German)
Deutsch (German)
Glossary
Atonality
By prefixing the alpha privativum, the term atonality indicates the absence of tonality. Ci-analysis enables the definition of clear demarcation criteria necessary for a meaningful use of terms. From its perspective, individual chords lack a tonal steering effect if they either do not contain any ci or if they exclude all six K-structures by accumulating ci. Atonal as a result of the absence of ci are, for example, the ‘D7 without fifth’ c-e-bb or the augmented triad c-e-g#. All six K-structures are blocked, for example, by the five-tone chord c-e-f-g-ab. While an inserted ci-free chord does not obstruct a harmonic progression, it is abruptly interrupted by the named five-tone chord. The classification of a chord as atonal does not relieve the need to determine its effect on the subordinate tonal space.
Space of Possibilities
Ci temporarily rule out tonal stabilization in the assigned K-structure. The options that remain after inserting a chord or a sequence of chords is called Space of Possibilities. Even in classical harmony, its design is relevant for the choice of a function representative. The Classic tutorial explains what effect, for example, the effect which has the replacement of the subdominant (S) by an S6 or the addition of a minor or a major None to the tonal space.
Minor Problem
One of the unresolved schisms of music theory relates to attempts to derive the minor triad from the major triad formed in the overtone series. By implementing the K and S axes in the twelve-tone scale, the problem is solved mathematically and geometrically in a simple and flawless manner: major and minor triads are mapped to each other under both K and S. The mapping formulas are: 3 – x = K (x); 9 – x = S (x). This can be seen from the following diagrams: C major (red) is shown under S on D minor (orange) and under K on A minor (green); A flat minor under S in F sharp major (blue). The fundamental tones of the major tones are abstract on the numerical values 0 and 6.
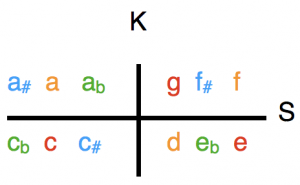
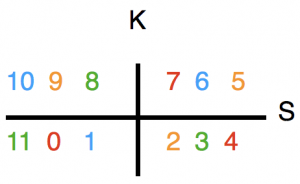
Complementary interval
In logic, elements, which exclude each other, are called complementary. In order to model his complementary series, Arnold Schönberg mirrored tones at an axis K inserted into the chromatic total. The tone K (x) obtained by mapping a tone x by K is separated from the other by inserting it in the other hexachord. The inserting of x in the first hexachord of the series determines thus the inserting of K (x) in the second. The two elements (tones) of such a complementary interval (ci) are mutually exclusive. As long as music is located in a specific K-structure, the ci assigned to it are not allowed not appear.
In musicological terminology, intervals that complement each other to the octave, such as fourth and fifth, are called complementary intervals as well. To avoid misunderstandings, the abbreviation ci (= complementary interval) is used for complementary intervals generated by K. We have thus to distinguish between an interval, which is complementary to another interval and an interval, whose components are complementary to each other (ci).
Tonal path
Each of the twelve major and twelve minor keys is located in one of the six K-structures. A prerequisite for the attachment of a key is the avoidance of the ci of its K-structure, combined with the exclusion of the five other K-structures by appropriate ci. The definition of a certain K-structure resulting from a sequence of chords becomes visible in the tabular overview as a tonal path. A suitable tone selection is also required to determine one of the four keys of a K-structure. With a standard cadence, the modeling of the tonal path and the tone selection are combined in one process. The nineteenth century, in particular, gains expanded display options from the separation of the two steps. In the model below, the tonal path of the C major cadence is highlighted in blue.
Term
Explanation of the term

