Tutorials

This post is also available in: Deutsch (German)

Introduction

You can change rules, but not natural laws. However, there is a connection between the two, because rules often strive to coincide as far as possible with an effective but not precisely defined law. Such an approximation can also be stated in classical harmony. By opening up wide areas of the empirically encountered sound cosmos, it is an indispensable means of analysis and interpretation. Nevertheless, the extent of the unexplainable remains high. Ci-analysis is based on the tonality symmetry K and undertakes to significantly reduce the existing gap in interpretation without contradicting the results of traditional harmony.

Functional theory and the theory of the degrees focus on the major triad contained in the overtone series. The functional theory also bundles various triads into functional groups and arranges them in a hierarchical relationship. Frequently used models can be recognized quickly, deviations can be identified and their intention can be queried. Alternative chords are described terminologically as a modification of the reference triad. They are called augmented or diminished, or contain so-called altered tones. Intervals are often interpreted as incomplete triads, four-tone chords as extended triads.

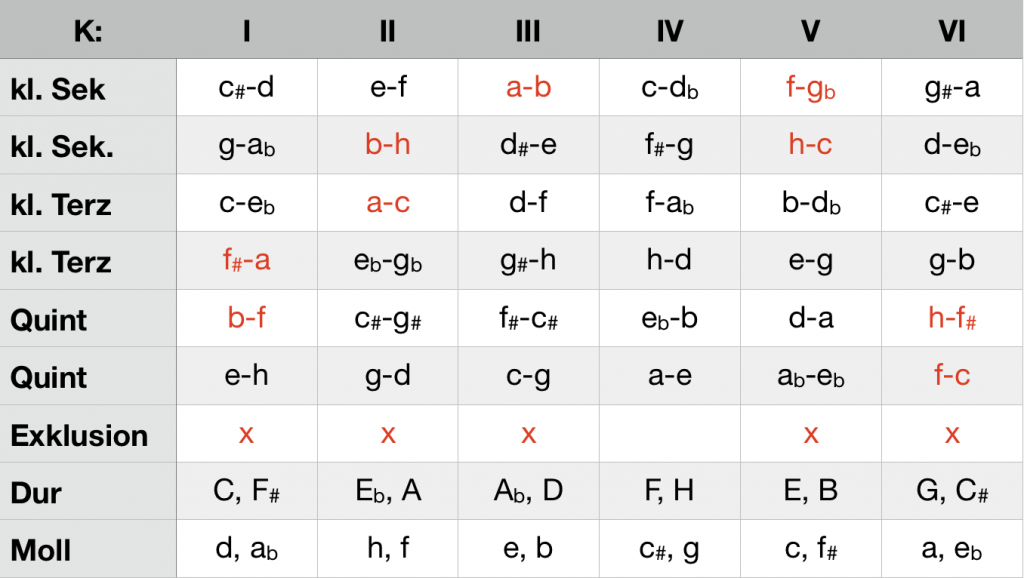
The systemic weaknesses of the triad-based analysis are evident: harmony starts with the interval, and the relentless attempts to derive chords from a three-tone master pattern obstruct the examination of the specific properties. Ci-analysis starts with the interval and elicits the tonal relevance of chords by evaluating the complementary intervals (ci) contained in each case. This enables a precise, objective determination of the tonal steering effect. For major and minor triads, it is calculated by adding the two ci contained in each.

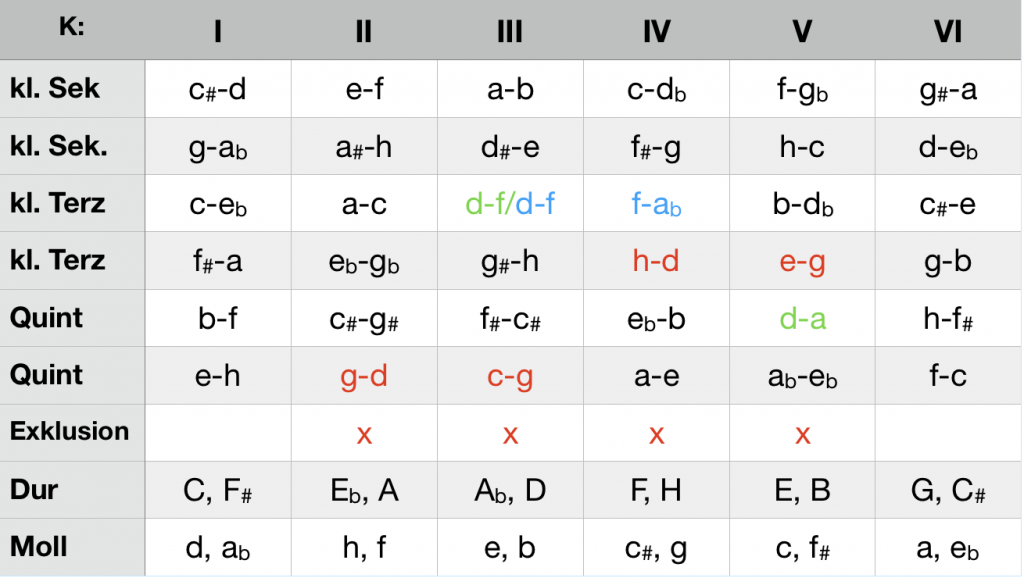
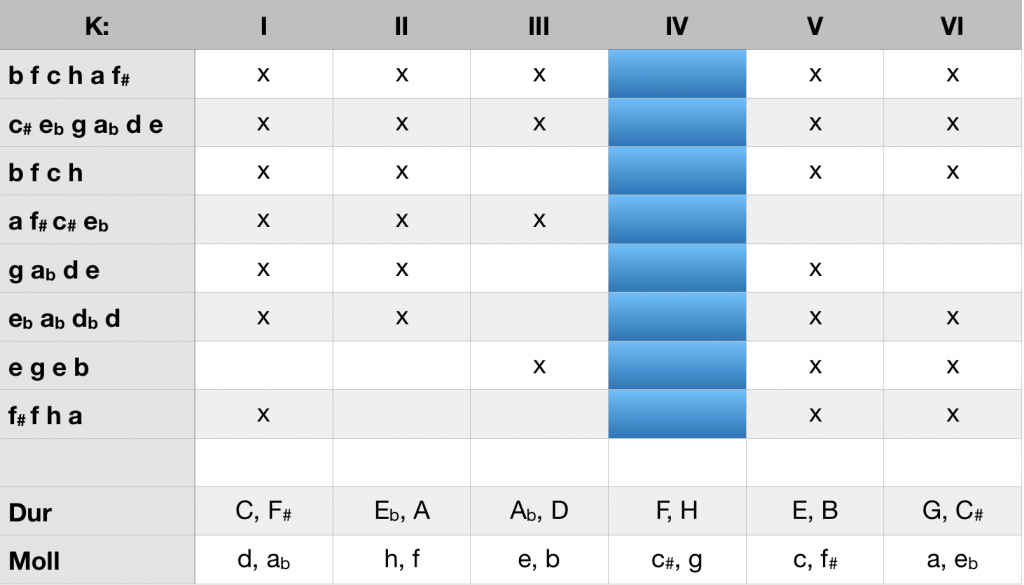
The securement of a key, familiar from conventional analysis, is joined with a gradual reduction of tonal alternatives. Ci-analysis maps this space of possibilities: Each ci requires the exclusion of a K-structure. The keys in this structure are temporarily excluded as the target of tonal progression. As explained in the guide, each K-structure is the basis of two major and two minor keys. The synopsis shows the six K-structures with their assigned keys and ci.

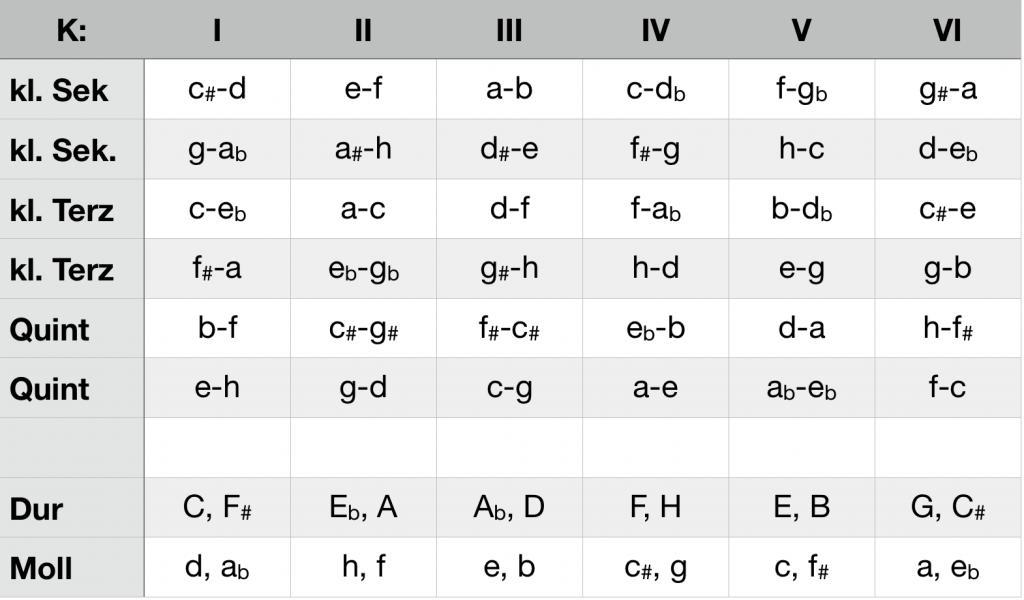
Synopsis of the keys and ci in the six K-structures

Starting from the triad f-a-c, for example, we can study the effects of allegedly marginal modifications on the subordinate tonal space. The triad f-a-c generates the ci f-c (K VI) and a-c (K II). If we add the pitch class d (f-a-c-d) we get furthermore the ci d-f (K III) and d-a (K V). The addition of a single pitch class means that two K-structures, and therefore a further eight keys, have been eliminated as possible targets. This also affects B flat major, a fifth lower. This explains the well-known subdominant effect of the sixte ajoutée. If we assign the subdominant function to the F major chord, the sixte ajoutée also changes the character of a mediant E major, since this key is located also in the now excluded K V. The composers of the 18th and 19th centuries, who enjoyed experimenting, were unaware of the underlying laws and depended on their aesthetic sensitivity. A single ‘wrong’ tone was enough to interrupt a harmonic progression or to modify the message radically. While conventional analysis only subsumes the achievement of E major in the context mentioned under the term mediantics, ci-analysis gives an indication why a relationship in thirds can occasionally be felt as an affirmative brightening or as an alienating break.

Instead of carefully extending the chord reservoir, we can use ci-analysis to quickly measure hypothetic spaces and to understand a composers decisions. Let’s illustrate this with a small experiment. For this we start with the now familiar triad f-a-c. From a K point of view, its function is to exclude K II and K VI. Which triads can also manage this? To answer this question we start with the ci e-f from K II. The complement of the pitch class e in K VI is c_#, the one f the c.

The triads e-f-c and e-f-c_# also initiate the exclusion of K II and K VI. If we proceed analogously with the other ci from K II, we get a total of twelve triads, which fulfill the task of the simultaneous exclusion of K II and K VI. In the adjacent music example, these twelve chords are used in a cadence instead of the subdominant function.

Cadence line with eleven K equivalents of the function subdominant

When playing the cadence line with the modified ‘subdominants’, we hear a peculiar mixture of affirmation and distraction. This is because the tonal path of C major always remains open, but the pitch class stock used is no longer limited to the scale of C major, but rather exhausts the twelve-tone total. The composers of the 19th century, trained in classical tonality, proceeded in a similar way: the expansion of the pitch classes available made the desired degree of ambiguity possible, while keeping a tonal path open at the same time allowed the preparation of a tonal goal. Since there are four keys located in each K-structure, a tonal fixation at the end still requires a limitation of the quantity of pitch classes. In this context, another remarkable property of the tonal space under K gains relevance. Another axis, designated S, is at a 90° angle to K. Arnold Schönberg, by the way, identified S as visible symmetry and placed a reference on the surface of the series of his op. 25. In K I there are the following mapping ratios under K and S for the pitch classes of the total:

The pitch classes of the C major triad (c e g (red)) are mapped on S to the pitch classes of the D minor triad (d f a (orange)), these under K on the F_#major triad (f_# a_# c _# (blue)), the latter under S on the A_b minor triad (a_b c_b e_b (green,)), A_bminor under K back on C major.

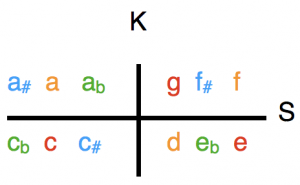
This result is interesting in several respects:

The four basic triads of the keys located in a K-structure are mapped to one another by the symmetries K and S.
Every pitch class obtained by mirroring at S belongs to the pitch class set of the key of the original triad.
By mapping major and minor triads on one another via the axes K and S, the question that has been debated for centuries as to how the minor triad can be derived from the major triad is answered in a binding manner.

Thus it becomes comprehensible why the triad remains an important means of representation even in advanced tonal compositions. As long as we are ‘on the way’, we can use all twelve pitch classes of the total and appropriate chords with 2 to 6 pitch classes when modeling tonal paths. Within the K-structure highlighted by a tonal path, however, the triad remains the most adequate means to document the final decision for one of the four keys located in this K-structure. At the end, if a certain level of tonal liability is to be preserved, emancipation from the triad comes to its natural limit.

Classics

Ci-analysis starting on the interval level already provides important detailed information about classical harmony. While the conventional theory of harmony based on the triad model only indicates the use of a function representative, ci-analysis documents the influence of a chord with regard to the subsequent tonal space of possibilities. This makes the compositional decision transparent for a specific function representative, raising awareness of the subtleties of the harmonic progression.

Standard cadence in C major

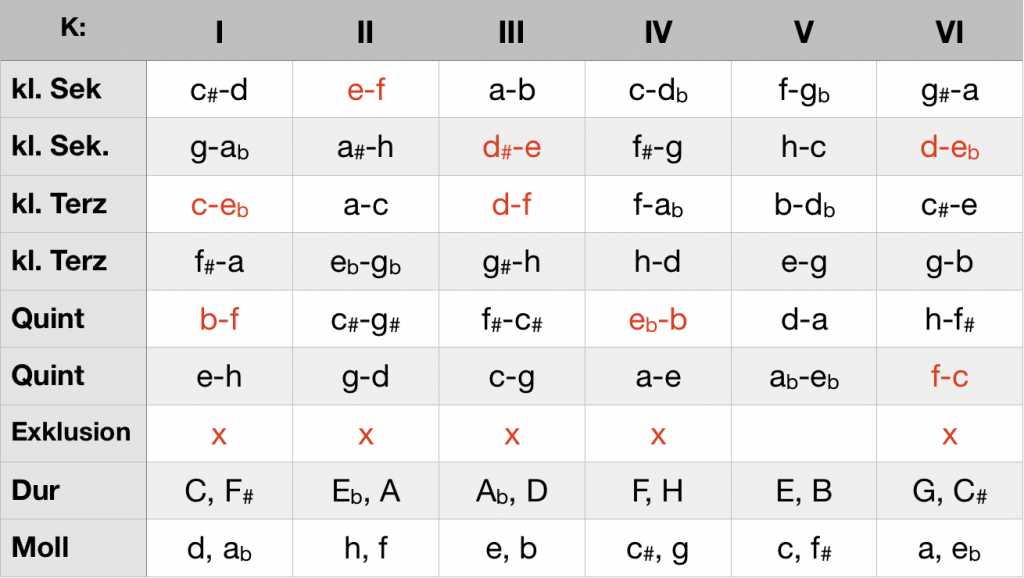
The triads c-e-g (T), f-a-c (S) and g-b-d (D) generate the ci colored red in the adjacent table. The sequence of these three triads successively excludes the K-structures II-VI as potential places of a tonal development, so that only K I remains. The standard cadence is probably the most efficient means of producing tonal clarity. On the one hand, five of the six K structures are excluded with the lowest possible number of triads On the other hand, the key aimed in the target structure is clearly determined by the pitch classes of its scale. Since in the specific case of the C major cadence two ci are generated in K II, the subdominant can also be represented by a minor triad (f-a_b-c) without affecting the tonal orientation. The ci a-c is then omitted, the ci f-a_b in K IV (blue) is added.

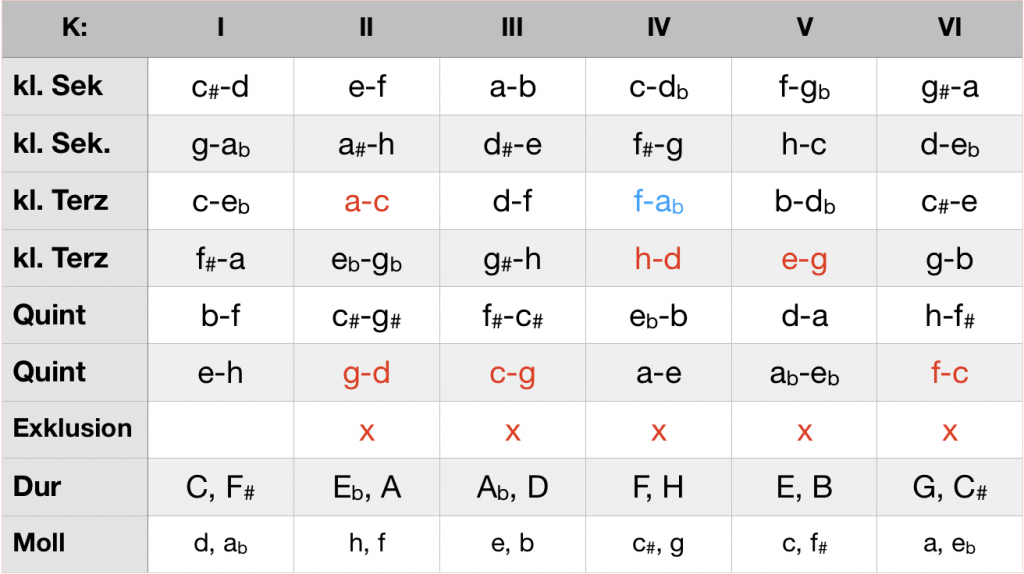
ci of the C major cadence

Standard Cadence in D minor

Each major or minor triad excludes two K-structures. A standard cadence thus generates six ci, which is why one of the five K-structures is excluded twice. In the case of a minor cadence, the ci formed by the basic pitch class and the third of the dominant is situated in the double-excluded K-structure. In the case of the key D minor, this is the ci a-c in K II. It is therefore not necessary for the tonal orientation. This allows the use of the major dominant preferred for melodic reasons (ci: c_#-e in K VI, blue). With regard to the possible conversion of the mode, the situation of the subdominant in the major cadence is therefore reciprocal to the situation of the dominant in the minor cadence.

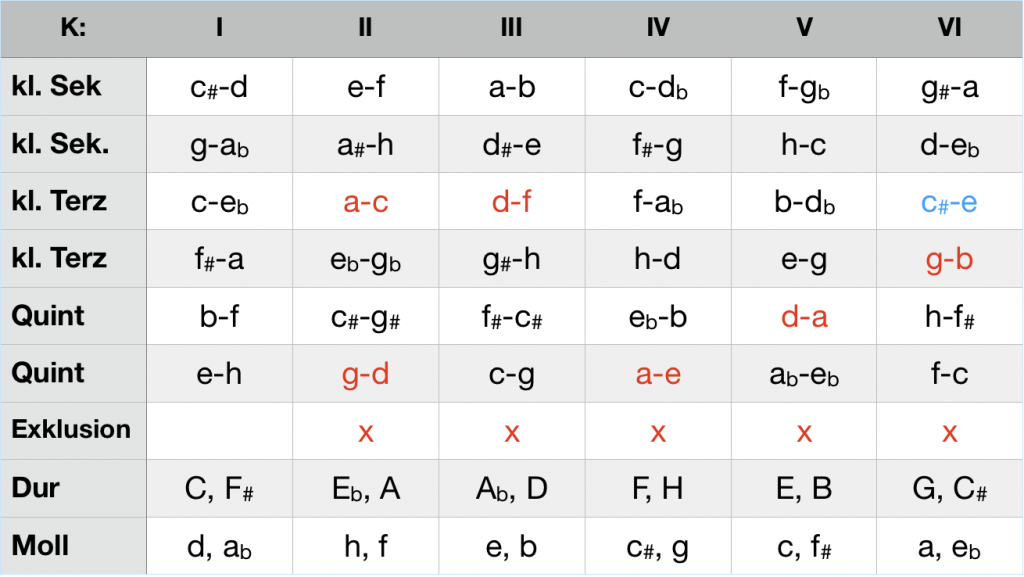
ci of the d minor cadence

Variations in the subdominant: S⁶, s⁶and sⁿ

Replacing the fifth by a minor or or major sixth in a subdominant triad affects the generated ci:

Major cadence:

In a major cadence, the ci a-c (K II) and f-c (K VI) are omitted due to the substitution of the fifth. This opens the K structure of the dominant (K VI). When using an S⁶ (f-a-d) we get instead the ci d-f (K III) and d-a (K V, each green). When using an s⁶ (f-a_b-d) we generate the ci d-f (K III) and f-a_b (K IV, each blue). In any case, the K-structure has already been excluded by another ci. The opening of the dominant K-structure facilitates the modulation to the upper fifth. Equipped with this information, we can check in concrete compositions to what extent these function representatives are used to prepare a modulation to the upper fifth.

C major cadence: S^{6 and}s⁶ facilitate a modulation to the dominant G major

Minor Cadence:

In the case of a minor cadence, the situation is somewhat different. The ci g-d in K II that is omitted when using an s⁶(new ci: e-g in K V) or sⁿ(new ci: e_b–b_bin K IV) leads to an opening of K II only in combination with a subsequent major dominant (omission of the ci a-c). This would pave the way for the major dominant. A modulation to the natural dominant A minor in K VI is not promoted when replacing the fifth by a sixth.

D minor cadence: s⁶ und sⁿdo not favor a modulation towards the dominant A minor (K VI)

Characteristic dissonances

The so-called characteristic dissonances serve to increase the functional effect of specific chords. In the case of the subdominant this is the sixte ajoutée, with regard to the dominant the minor seventh. The D⁷ is occasionally extended by a minor or a major ninth. The consideration of the generated ci indicates the reason of the effect.

sixte ajoutée

In the table below, the ci generated by the chords f-a-c-d (s⁵⁶ of C major, red) and g-bb-d-e (s⁵⁶ of D minor, blue) are highlighted in color. In both cases, the ci in K V (d-a or e-g) generated by the sixte ajoutée blocks the way to the respective fifth below (B major; C minor). Moving on in the circle of fifths is only possible in the direction of the respective tonic.

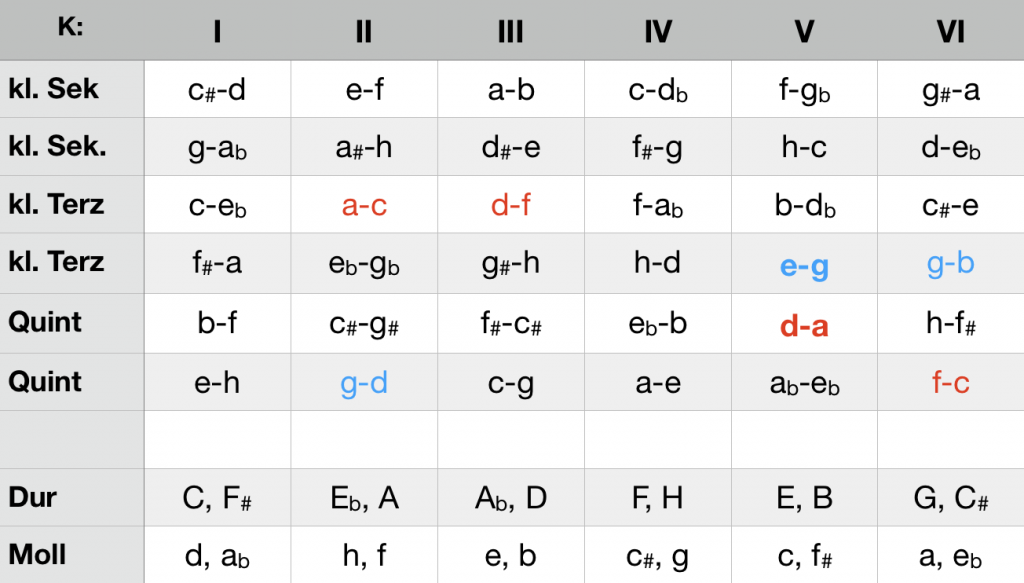
Control of the direction of movement by the sixte ajoutée

Dominant seventh chord and dominant seventh-ninth chord

In the table below, the ci generated by the chord g-b-d-f (D⁷ of C major) are marked in red, the ci generated by adding the minor ninth green, the ci generated by adding the major ninth blue. The ci d-f in K III (red bold) generated by the minor seventh blocks the way to the upper fifth in D major. As in the case of the sixte ajoutée, moving on in the circle of fifths is only possible in the direction towards the tonic. Of course, the direction of movement in the circle of fifths changes. Since the addition of the major ninth excludes the K-structure of C minor (ci d-a , K V) , the addition of the minor ninth that of C major (g-a_b, K I), the selection of the ninth also decides on the mode of the following tonic.

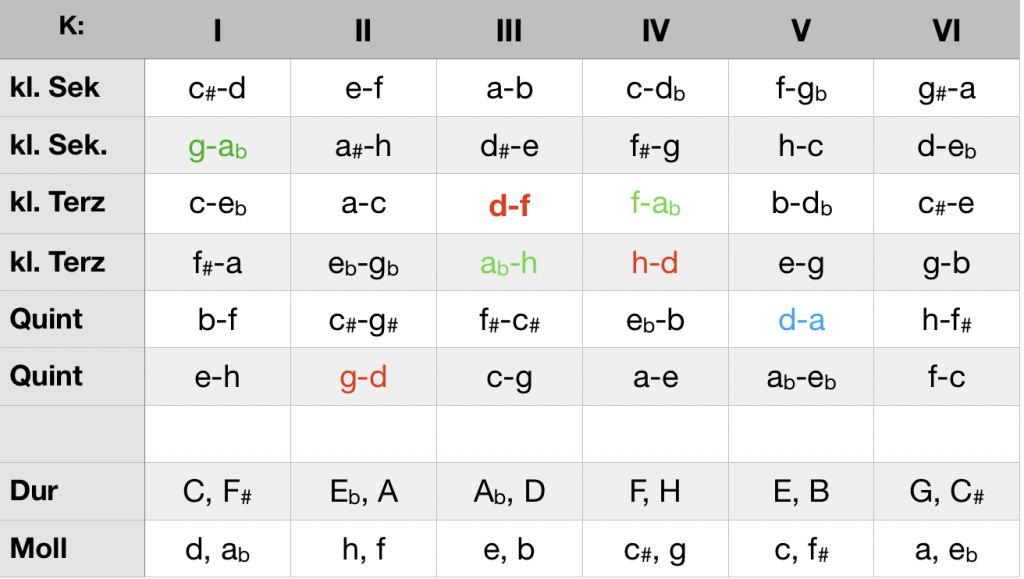
Control of direction of movement and mode by seventh and ninth

In fact, compositional practice rigidly follows the conditions of the tonal space under K:

A major chord with a minor seventh initiates a movement towards the lower fifth.
A D⁷with a minor ninth leads to a minor tonic.
A D⁷ with a major ninth leads to a major tonic.
If a dominant seventh chord with a minor ninth is followed by a major triad, the latter is not a target, but a stopover.

Conclusion

Based on the hidden symmetry K, ci-analysis provides a supplementary access to the allegedly familiar harmonics: its rules and the concrete use of the numerous function representatives can be derived from K without exception. First of all, this is a fascinating result under the auspices of music theory. Furthermore, it has profound implications with regard to the interpretation: We can now also trace subtly initiated harmonious developments back to their respective beginnings. While the individualization of music during the 19th century restricts the assignment of functions, ci-analysis gains in importance for understanding the harmonic progression.

Romanticism

The development of harmonics in the 19th century is characterized by two trends. On the one hand, pitch classes not belonging to the scale are increasingly used to outline the tonal path. On the other hand, the dealing with new topics favors alternative scenarios of harmonic progression: the tonic is no longer necessarily the starting point or goal. Frequently, the tonal concept can only be deduced from the synopsis of functional and ci analysis.

In the 19th century, music is characterized by the contrast between individualization and objectification. The harmonics, which are particularly affected by this, are trying to detach from classical patterns and at the same time use them as a reference: the individual is defined through its distance from the norm. The traditional theory of harmony states the deviations without being able to name reliable criteria for the interpretation of their content. In order to better understand the intention of a harmonic development, it is helpful to look at the space of possibilities and its tonal paths.

A excellent example of the sublime amalgamation of a classical pattern with Romantic harmony is provided by bars 1-16 of Frédéric Chopins Waltz in C sharp minor op. 64. A functional analysis first confirms the immediate impression: an abundance of double and intermediate dominants, intermediate subdominants and ellipses causes a longing and striving in all directions. The tonic seems to be little more than the soon-to-be abandoned starting point, and the constantly changing but never fixed tonal intermediate destinations evoke the suggestion of a constant circling in the ballroom.

Frédéric Chopin, Waltz C sharp minor op. 64,2; bars 1-16

A fixing of the basic key in the classical sense cannot take place, because the subdominant F sharp minor, apart from a ephemeral suggestion in bar 10, 3rd beat, does not appear in the score. In the Theory of Tonality (cf. p. 74ff), functional analysis is contrasted with a ci-analysis and reveals the other side of the harmonic progression: after four bars in the K-structure of the tonic (striving towards the dominant), the tonal path in bars 5-8 is situated in the K-structure of the never-attained tonic parallel E major. Afterwards it goes back to the K-structure of the tonic that is not irritated by a single ci in bars 9-16. It would already suffice to present the double-dominant D-sharp major in measure 14 with its fifth to destroy the effect of an undisturbed K-structure (ci d_#-a_# in K IV). One can easily convince oneself of this by trying out this variation. The basic key of C-sharp minor, which appears occasionally, is not fixed in the traditional way, but by keeping its K-structure open. The sense of harmonic progression can be deduced from the simultaneous consideration of functional analysis and tonal paths.

A master in shaping clear tonal paths is Claude Debussy, whose impressionistic style refines the romantic concept. In his prelude “…La fille aux cheveux de lin” Debussy makes repeatedly use of the fact that a pentatonic section, in lack of semitones, does not establish a key, but can make a decisive contribution to tonal progression through the ci it contains. In bars 8-16 of the Prélude there is an ingenious juggling with the bivalence of pentatonic sections. At the beginning of this section, the music oscillates between a G_b⁷ acting as (D⁷)[S] and a double-dominant A_b⁷. The subsequent bars are heading to and finally reach the tonic G_bmajor, which is however not perceived as a definite goal.

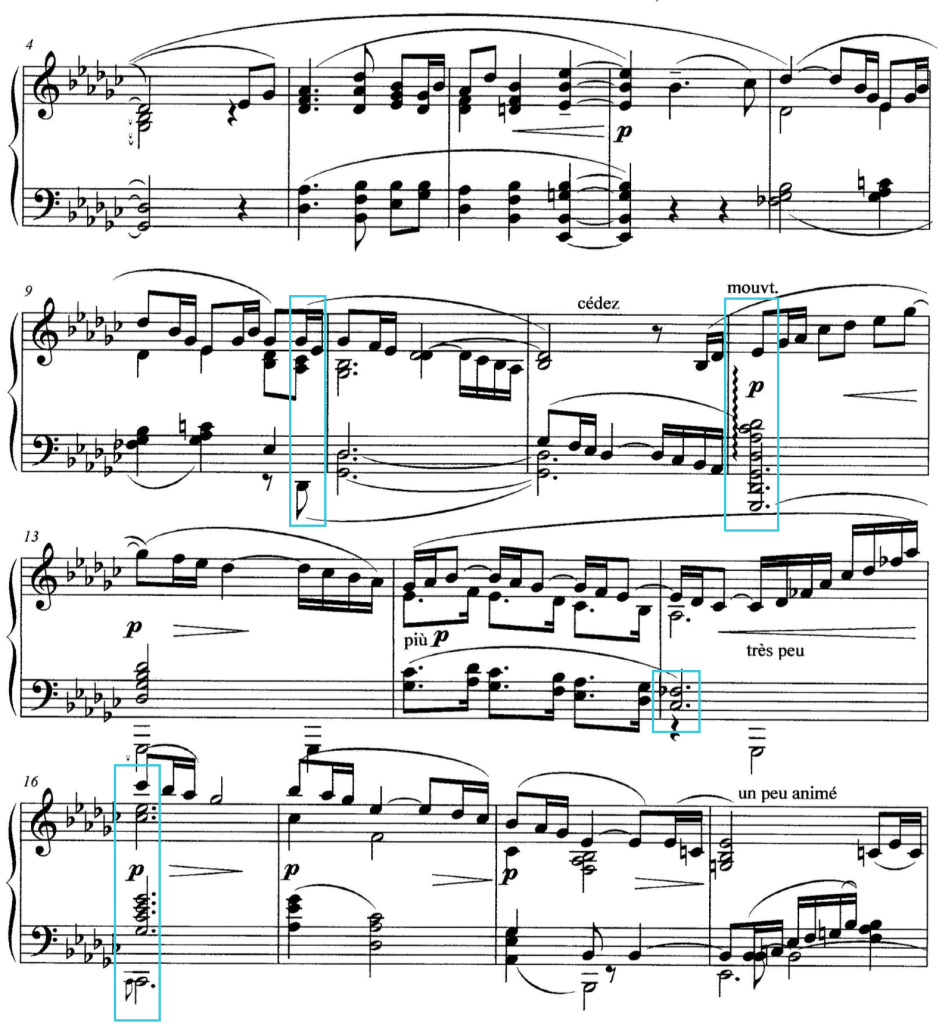
Claude Debussy, La fille aux cheveux de lin, bars 4-19

The reason becomes apparent when looking at the ci. The D flat major seven-ninth chord (bar 9, last 1/8 and bar 12, 1st beat, here as part of a pentatonic section) lacks its third f. This pitch class would be necessary, however, to shape, together with the pitch class a_b,the ci f-a_b thus excluding K IV, the K-structure of the subdominant. In bars 9-14, therefore, both K I and K IV remain open. In bar 15 another pentatonic section is then traversed, and the ci c_b -f _b excludes K I.

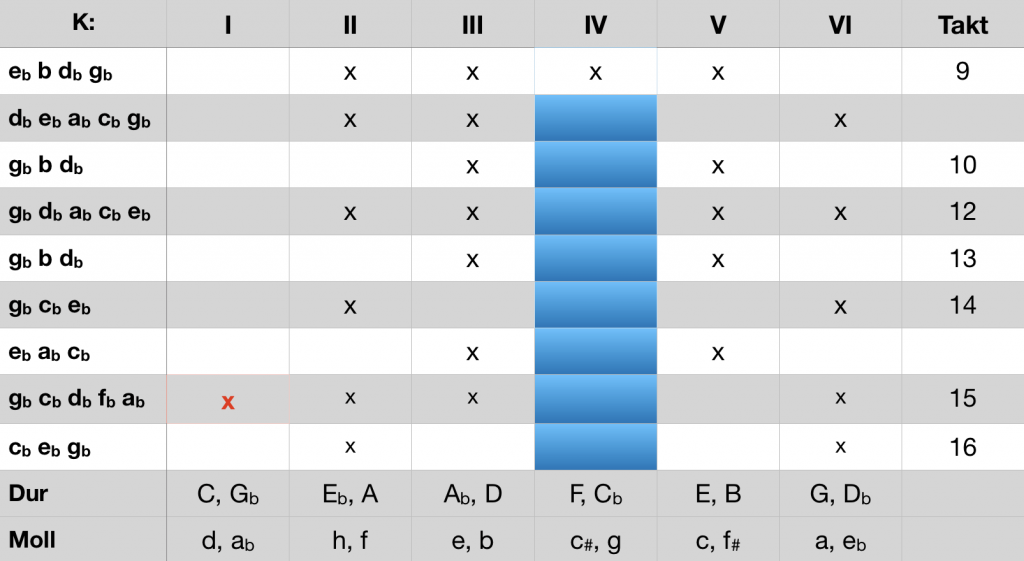
Exclusion of the alternative K structure I by a pentatonic section bar 15

At the beginning of bar 16, C_bmajor actually presents itself as the gently gleaming winner of the sublime duel for tonal primacy. It is worthwhile to make an experiment by using the tones of the section bar 12 also for the ascent bar 15. The C_b major bar 16 does not sound wrong then, but it has lost its magic.

The temporary keeping open of two K-structures, as celebrated by Debussy, can be a powerful tool for creating romantic topoi: an expression of a necessary decision at the crossroads, or a symbol of uncertainty whether fate will bring joy or sorrow. Keeping the major and minor structures of a key open is given by combining minor subdominant and major dominant. To keep only the two target structures open, either the subdominant must be supplemented with a sixte ajoutée, or the dominant with a minor seventh.

Since tritone transpositions of a chord generate identical exclusions, the moment of uncertainty can be enhanced by replacing one of the two functions mentioned – minor subdominant or major dominant – with its tritone transposition. In the table on the right, the situation is illustrated by the example of a cadence_# directed to C – or alternatively F_#(major or minor). The chords available for selection according to the criteria mentioned above always leave the K-structures of C major (K I) and C minor (K IV) open.

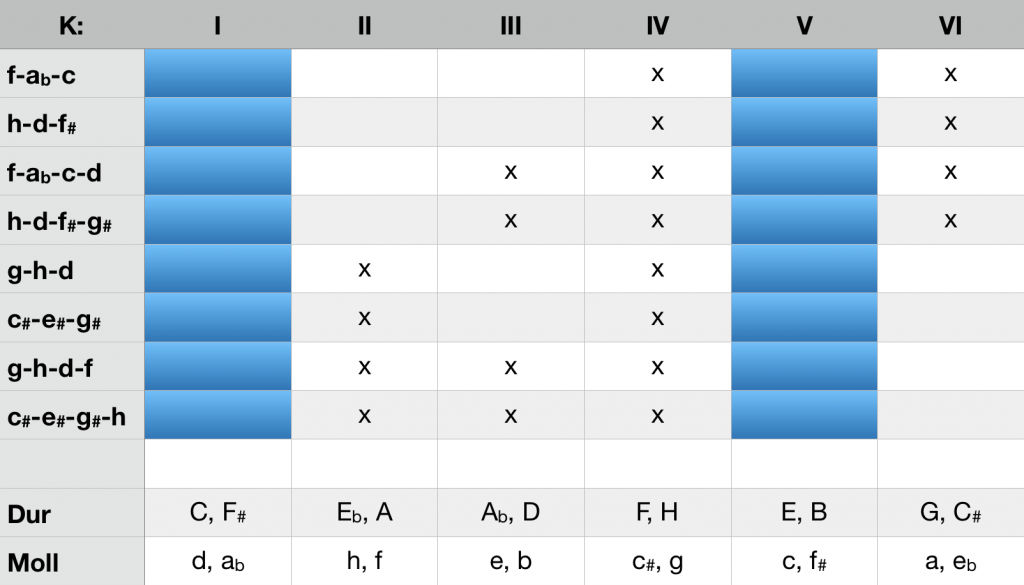
Chord inventory for keeping simultaneously open the K-structures of C major\F sharp major and C minor\F sharp minor

The alloy of an uncertainty about the processing of the tonal path, combined with the de facto tritone transposition of a function representative, can already be found in bars 33-45 of the first movement of Ludwig van Beethoven’s Sonata in E_bmajor op. 31,3 (1801/02). At the beginning of bar 33, the head motive of the main theme appears in a minor key and abruptly interrupts the affirmative and vigorous gesture of the beginning of the movement. Starting from the chord a_b-c_b-e_b-f bar 34 we pass in bar 35 to f-c_b-e_b-a_b, model of the famous Tristan chord (f-b-d_#-g_#). The chord is a harmonic enigma, because if one interprets the pitch class e_bwhich finally drops to the d, as a fourth suspension, the previous subdominant is to be interpreted as a D^v.

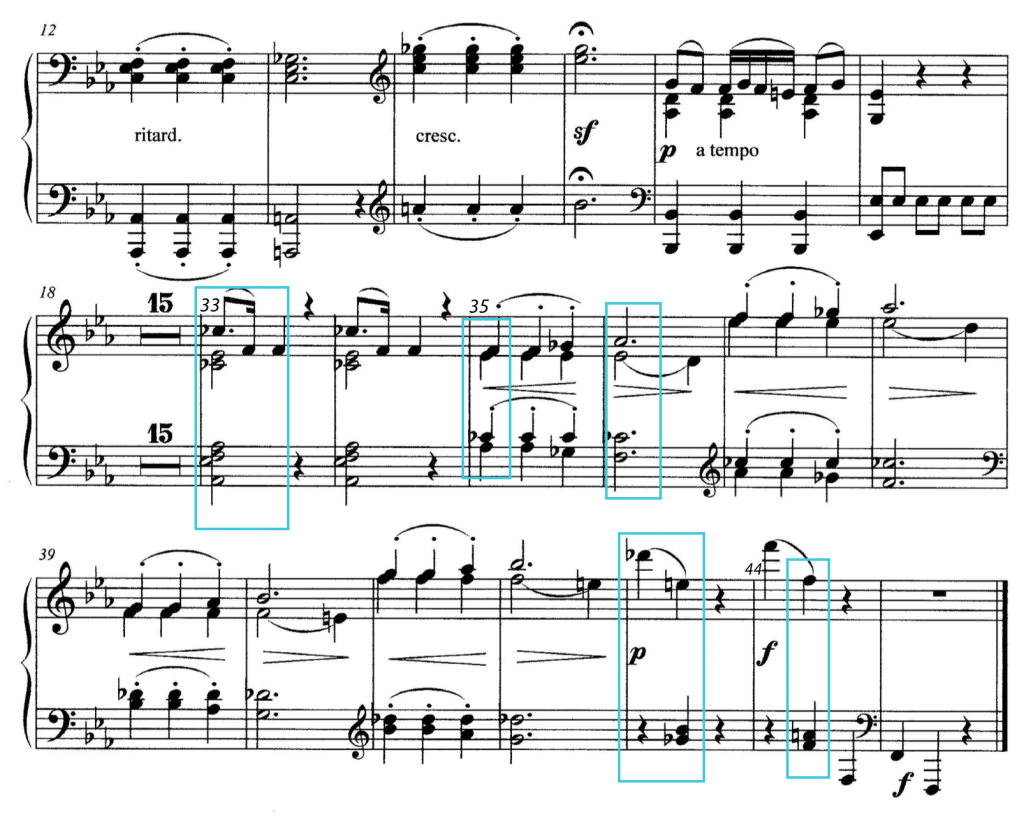
L. van Beethoven, Sonata E flat major op.31,3; 1st. movement, bars 12-17 and 33-45

The ci-analysis is revealing in several respects:

In bars 33-38, the tonal path processes in K I, the structure of A-flat minor. Its triad points to the upper fifth by means of the sixte ajoutée without a corresponding progression. There is a conflict between the intended harmonic direction and the de facto immobility.
By a sudden shift, the state of tensed statics bar 39 is transfered to K III. The deflection to F major is then not achieved by a development, but is forced bar 43 by suddenly inserting a G_b⁷.
The exclusion of F minor is not achieved by a ci in its K-structure, but by the final inserting of the major third bar 45: demonstrative act of will instead of harmonic development.

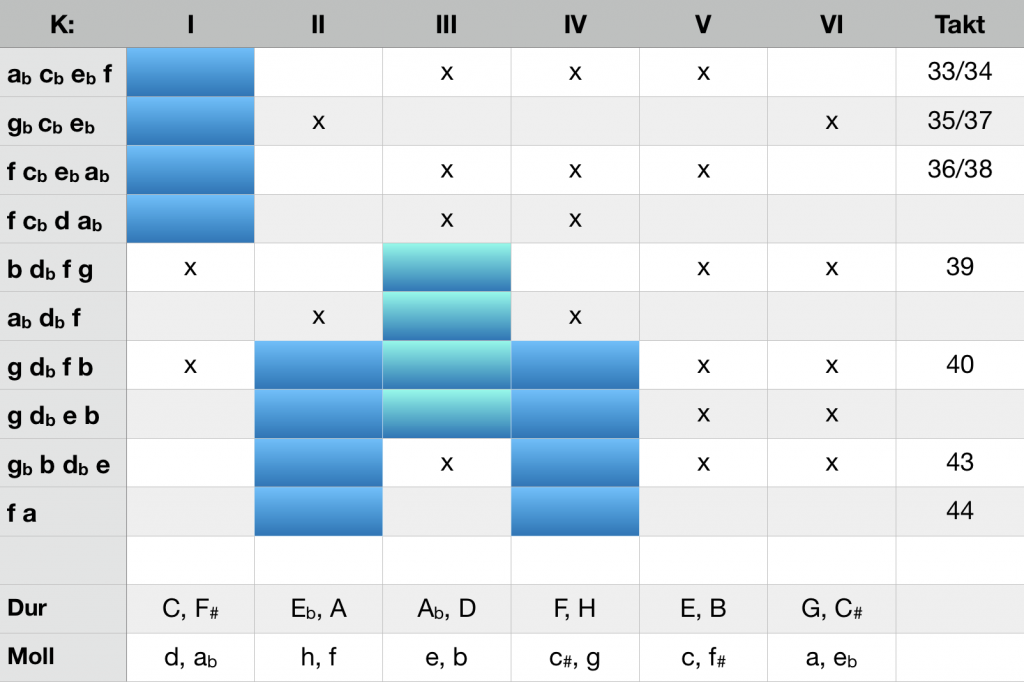
Beethoven’s primeval form of the Tristan-chord: deliberate placing instead of harmonic development

For measures 33-45, a combination of functional and ci-analysis points to a state of sudden depression from which Beethoven almost violently escapes. On closer inspection, this passage is far more than just a pleasant minor contrast in the midst of good-humored E_bmajor activity.

At the beginning of the prelude to his opera Tristan, Richard Wagner ties in Beethoven’s Tristan germ cell in several respects, but develops a very individual statement from it. The tonal material of the initial chord in bar 2 corresponds to the tritone transposition of a D minor chord with sixte ajoutée. The first phrase closes bar 3 on an E⁷. The ci of this romantically alienated cadenza without harmonic solution leave the K-structures of A minor and A major open. By the way, by forwarding the melody from the tone g_#to the note a bar 2 all ci are eliminated, even the chord e-g_#-d-a_# is ci-free. The situation is analogous for the following two segments, each separated by breaks: Between the two chords serving as tonal frames, the tonal development remains ci-free, thus without tonal steering effect. The second segment (bars 5-7) is a transposition of a minor third upwards of the first segment. Possible targets here are thus C minor and C major. In the third segment, the tonal material of the original chord is transposed by a tritone, the final chord is transposed up a major third (B⁷). As a result, not four but five K-structures are now excluded, leaving K V as the structure of E major. The synopsis shows that, after the Tristan chord has been exposed, the E major structure K V was kept open constantly, notwithstanding the goals that were sketched but never achieved. Not merely for Wagner E major was the outstanding key to symbolize love. The idea of salvation by love obtains its obvious expression in these harmonically highly complex bars.

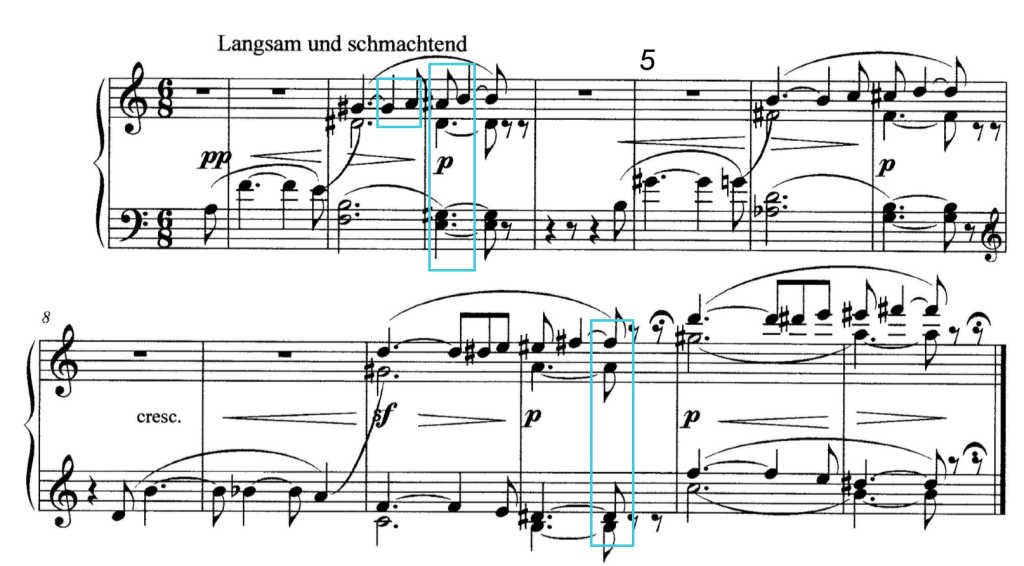
Richard Wagner, Tristan und Isolde, introduction, bars 1-13

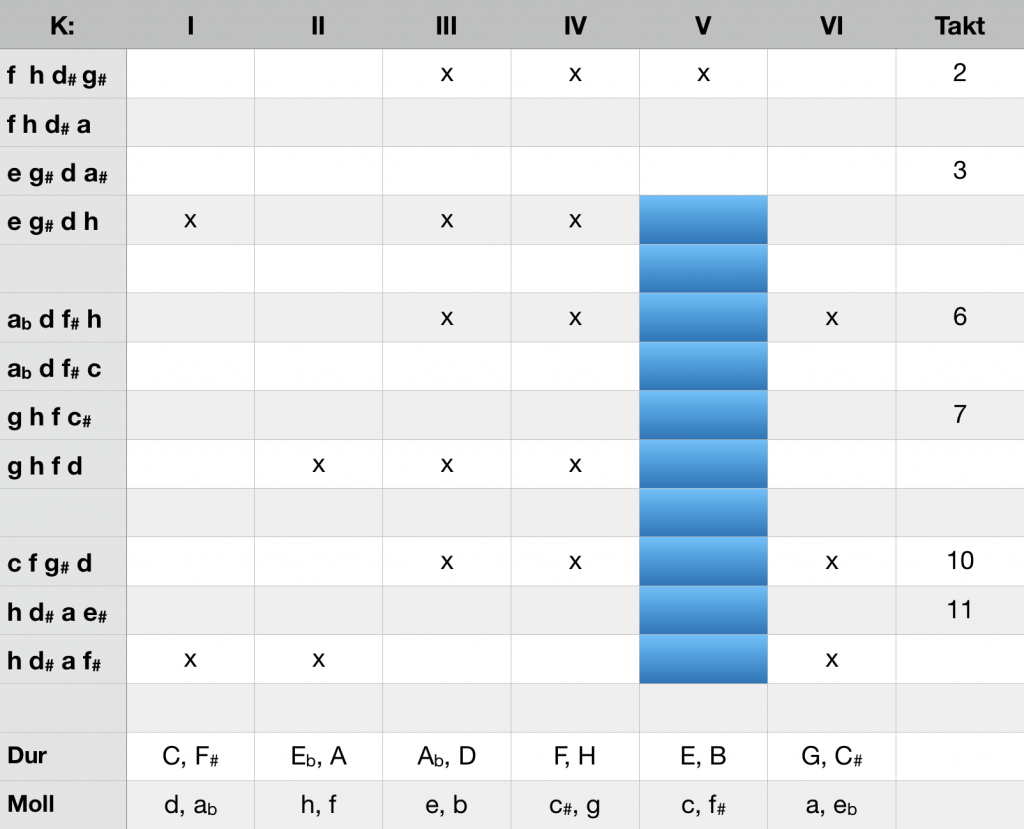
Tonal frame and atonal core, salvation by love in K V: The magic of the Tristan introduction is complex

Among the works examined in the Theory of Tonality, the following 19th century composers, among others, show a marked tendency to contour clear tonal paths: Franz Schubert, Felix Mendelssohn Bartholdy, Franz Liszt. In Peregrina I of Hugo Wolf, also analyzed there, on the other hand, a strong irritation or even the loss of tonal orientation can often be detected, always connected with a special mental situation or certain key words. Ci-analysis is a gateway to this world. The real adventure begins when we learn to interpret the results.

Schönberg

Arnold Schönberg uses the hidden symmetry K to divide his rows into complementary hexachords. The separation of the hexachords in the score gives him the occasionally used opportunity to compose tonal sections. The method is further safeguarded by the selection of tonally potent basic dichotomies. With his twelve-tone method, Schönberg provides a fascinating synthesis of a tonality which is emancipated from the triad on the one side, and atonality on the other.

As a composition teacher, Arnold Schönberg dealt intensively with questions of harmony. With its approximately 500 pages, his book Harmonielehre is beyond the usual scope. Of course, the theorist Schönberg was aware that the composers of the 19th century used a large number of non-scale pitch classes and chords which were far from the cadence without necessarily suspending the harmonic progression. He summarizes this in a so-called thesis: „Harmoniefremde Töne gibt es nicht, sondern nur dem System der Harmonie fremde.“ (H, S. 463) We explained the cause of this harmonic functioning beyond functional theory in the tutorial treating Romanticism When orienting to a target tone space (i.e. K-structure), you are free to choose the tones as long as you avoid generating ci of the target tone space. Using all twelve pitch classes of the total, one can therefore limit the range of what is tonally possible to a single K-space, initially without letting the tonal goal appear. In ignorance of the symmetry K, the composers of the 19th century were dependent on their sensitivity when expanding the classic harmony model. Regardless of all individualizations, the triad remained thus the central instance of harmony.

To use the chromatic total unreservedly, a new system was required which equated the tones categorized as out of harmony with the pitch classes of the scale. This equality was achieved with the transition to dodecaphony. Arnold Schönberg, mastermind of the new composition technique, immediately integrated the tonality symmetry K into his concept. His complementary series, all aligned with K, gave him the opportunity to compose dodecaphonic and tonal simultanously. Since he passed on the technology as such, but did not unveil the tonal implication of K, the latter was neglected when studying his oeuvre. Actually, composing with complementary series ties in directly with the tonal innovations of the previous 19th century. However, research concerning Schönberg has arranged in the atonality corner and is hesitating to leave it.

The first prerequisite for systematically composing dodecaphonic-tonal is the shaping of a complementary series. Having regard to the axis K, this is basically simple. First you have to decide where to insert K in the chromatic total. Afterwards, for each pitch class x that is placed in the 1st hexachord of the series, its complement K (x) is assigned to the 2nd hexachord at any point. As long as the two hexachords are then kept apart in the specific composition, no ci of the underlying K structure are generated: the door to composing tonal is open. It is closed by superimposing the two hexachords. As almost to be expected, Schönberg makes use of this opportunity on occasion by composing tonal by holding apart, or atonal by layering complementary hexachords.

Complementarity is an important requirement, but not a guarantee of tonality. To emphasize a latent tonic in the composition, it is advisable, for example, to arrange the pitch classes of its triad in the same hexachord; and at the same time to weaken the tonal antagonist by separating it from the pitch classes of its triad. There exist also four complementary basic dichotomies that cannot completely exclude the five remaining K structures. The Theory of Tonality proves (p. 111f) that Schönberg actually chooses basic dichotomies with a maximum tonal potential for compositions with a decidedly tonal concept such as op. 33a and op. 42.

We would like to begin by using the example of the Piano Piece op. 33a. We demonstrate how Schönberg proceeds in designing a series and how he exploits its tonal potential.

The basic series and its inversion have the following shape:

R: b_bf c b a f_# | c_# e_b g a_b d e

U: e_b a_b d_b d e g | c b_bf_# f b a

The K-axis of the basic series is situated between the tones c and d_b. One can comprehend this by coloring the tones of the 1st hexachord, for example:

g a_b a b_bb c | c_# d e_b e f f_#

When exposing the pitch classes of the first hexachord into a six-tone chord, the following ci are generated:

Nine ci are thus generated, only K IV remaining open. If we would repeat the experiment with the 2nd hexachord, we would get other ci but identical K-structure exclusions. In order to privilege one of the four potential tonics in a K-structure, it is recommended to combine the tones of the respective triad in one of the hexachords, together with the basic pitch class of the tonal antagonist. This can easily be illustrated when looking at the 1st hexachord of op. 33a: It contains the pitch classes of the F major triad and the pitch class b, the major third of which is d_#/e_b in the 2nd hexachord. The tonal antagonist B major is separated from its third by the hexachord border and is therefore disadvantaged.

The latent tonic F is also indicated by the initial ascend of fifth with the series tones 1-3 (b_b-f-c) and secured by another inventive measure. Schönberg makes sure that even if the series is divided into tetrachords, no ci in K IV are generated:

Exclusions of the hexachords and the tetrachords op. 33a

The second tetrachord of the inversion, e-g-c-b_b, contains the pitch classes of the D⁷of F major. In fact, op. 33a starts with the vertical exposure of the tetrachords of the basic series and its inversion, and with the C⁷as the penultimate chord it presents an original harmonic reminiscence:

Arnold Schönberg, piano piece op. 33a, bars 1-2

In the Theory of Tonality a ci analysis of op. 33a is presented. According to it, the K-space of F major remains open in bars 1-2, 6-11 and 37-40. We get the following structure:

bars 1-2 tonal – 3-5 atonal – 6-11 tonal – 12-36 atonal – 37-40 tonal

Broadly speaking, a tonal beginning and ending are used as a frame in relation to the atonal inner part. The activation of the tonal option has a formative intention.

Analyzes of op. 33a point to structural parallels to the sonata form; highlighting Schönberg’s efforts to relate tradition and innovation. This is even more evident in his piano concerto op. 42, and again the activation of the tonal option plays a prominent role.

When looking at the basic series of op. 42, the exposure of the B_bmajor triad (b_b-d-f, pitch classes 2-4 of the series) immediately attracts attention:

e_bb_bd f e c | f_# g_# c_#a b g

As almost to be expected, the series is based on the K-structure V (K axis between pitch classes b and c), which is the base of B_bmajor, as can be easily demonstrated with our small test:

f_#g g_# a b_bh | c c_# d e_b e f

Arnold Schönberg, piano concerto op. 42, bars 1-4

When exposing the pitch classes of the first hexachord into a six-tone chord, the following ci are generated:

ci of the 1st Hexachord in the series of op. 42

The listing of the ci confirms B_bmajor. Compared to op. 33a, which was composed more than a decade earlier, the tonal potential of the ‘tonic’ is even more pronounced: the first hexachord not only exposes the B_bmajor triad openly, it also contains the tones 1-5 of the B_bmajor scale. The only pitch class not belonging to this scale is the potential tonal opponent e, which lacks a tonal potential due to the isolation from its triad tones g_# and b in the 2nd hexachord. Such details prove the further increased power of disposal regarding the tonal potential of complementary series.

In the so-called “secret program” of op. 42, Schönberg notes “life was so easy” for the first movement, outlining a comparatively light-hearted, yet irretrievable past. As in op. 33a, the first movement is oriented towards the sonata form. Actually, Schönberg matches the tonal option with the traditional form in order to convey the message: while remaining in the basic series and separating the hexachords, the K-structure of Bb major remains open in bars 1-16. The mood of the “life was so easy” is effectively supported by a strong approximation to a tonic B_b. In the recapitulation starting bar 133 the exposure of the theme is designed with the pitch classes of the basic series, but for the accompaniment frequently changing transpositions of the basic series are used, so that the tonal basis shifts beneath the feet of “easy life”.

The Theory of Tonality shows in detail how Schönberg uses the relationship between tonality and atonality for shaping the message in op. 42. Knowledge of this fact is essential for an interpretation. It is interesting in this context that the end of op. 42 is not tonal. The future imagined by Schönberg – “but life goes on” notes the secret program – does not presuppose an orientation towards a tonic. Nevertheless, even in his late years, Schönberg had no reservation about using tonality as a design tool.

App

Without tools, the identification of the ci in a chord, their assignment to the K-structures and the registering in a table requires a lot of time. The ci-App largely automates this process and radically reduces the time required.

The App ciAnalysis is designed for the iPad, requires the operating system iOS 10 or higher and can be obtained from the AppStore.

After opening the app, tiles indicating the analyses previously accomplished appear on the start page. We have three options to continue:

By clicking on a tile we open the associated document and can continue an analysis that has already been started or make changes.
If we want to edit the metadata of a document, we press successively Select document, the tile of the desired document, then dann Edit document. The editing of the metadata is discussed in the next section.
To start a new analysis, we press the + symbol in the upper left corner of the navigation panel. A form for creating a new document is displayed.

The app maintains the analyzes as individual documents that are stored on the iPad.

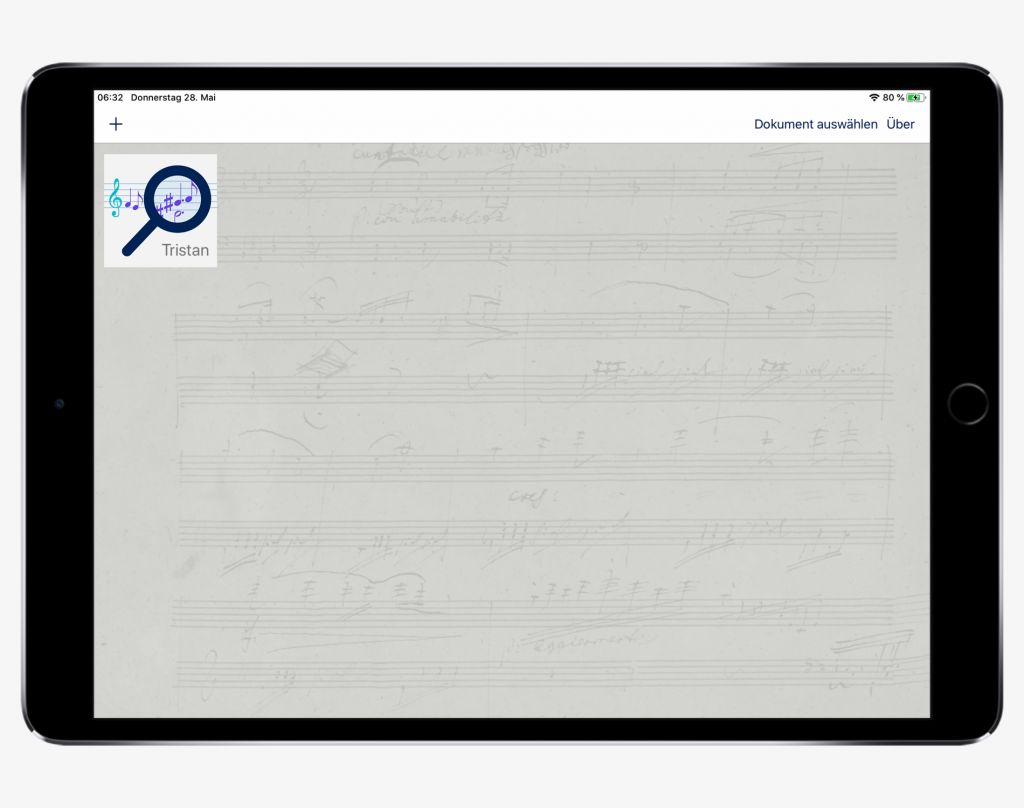
Start page with an analysis document

Creating a new document

First of all, it is necessary to assign file name. This name is determined after the document has been created! It appears later on the tile and should therefore be short and clear. The file name Tristan was chosen for the sample document.
The title may be a bit more detailed (here: the Tristan chord)
For Opus, if available, we register the number in the catalogue of works, in the example WWV 90 (Wagner-Werk-Verzeichnis).
If a work is known by a specific name, such as Beethoven’s Moonlight Sonata, this can be optionally entered in the Desription field (Bezeichnung). In the example the work from which the analysed example originates (Tristan and Isolde, Opera) is indicated.
For composer (Komponist) we enter the author of the analyzed composition (Richard Wagner).
In the Author field, we enter the author of the ci analysis.
If you wish to make a Comment, you can specify further details, for example if you are analyzing only a fragment from an extended work or if you want to add information about the purpose of the analysis.

With the exception of the file name, all information can be modified at any time. When we have completed the typing, we press the keyboard symbol in the bottom right-handed corner, then again on the bottom right-hand corner on Create (Anlegen). Now we can start the analysis!

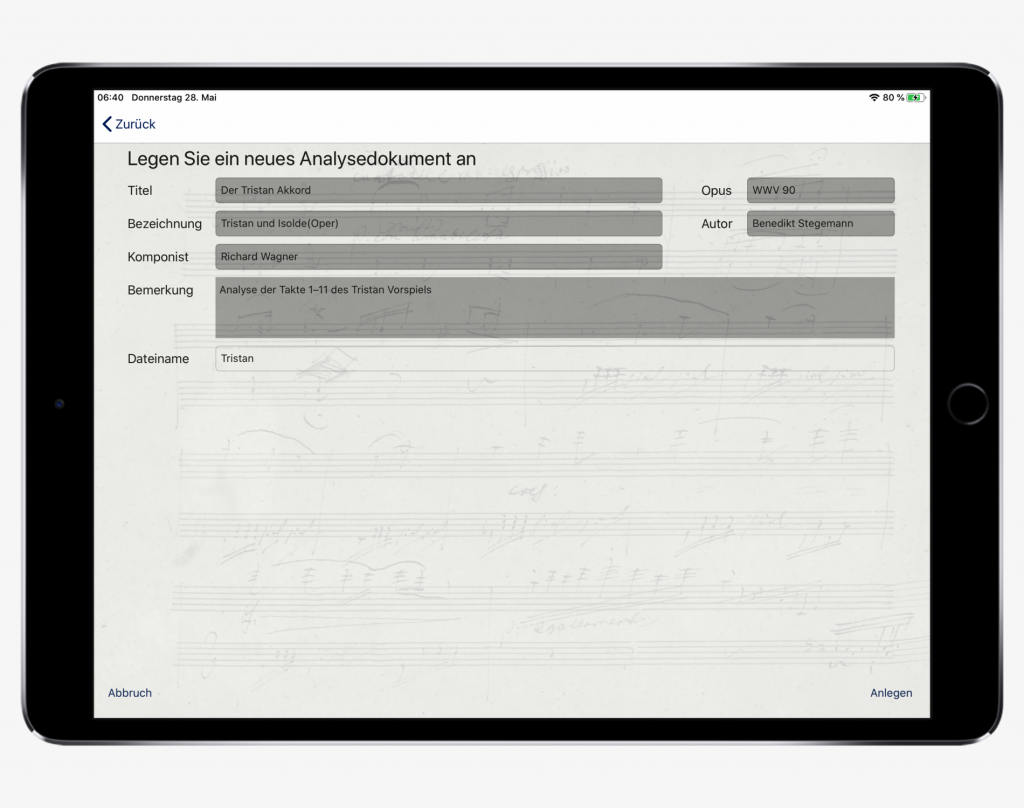
Input of the metadata

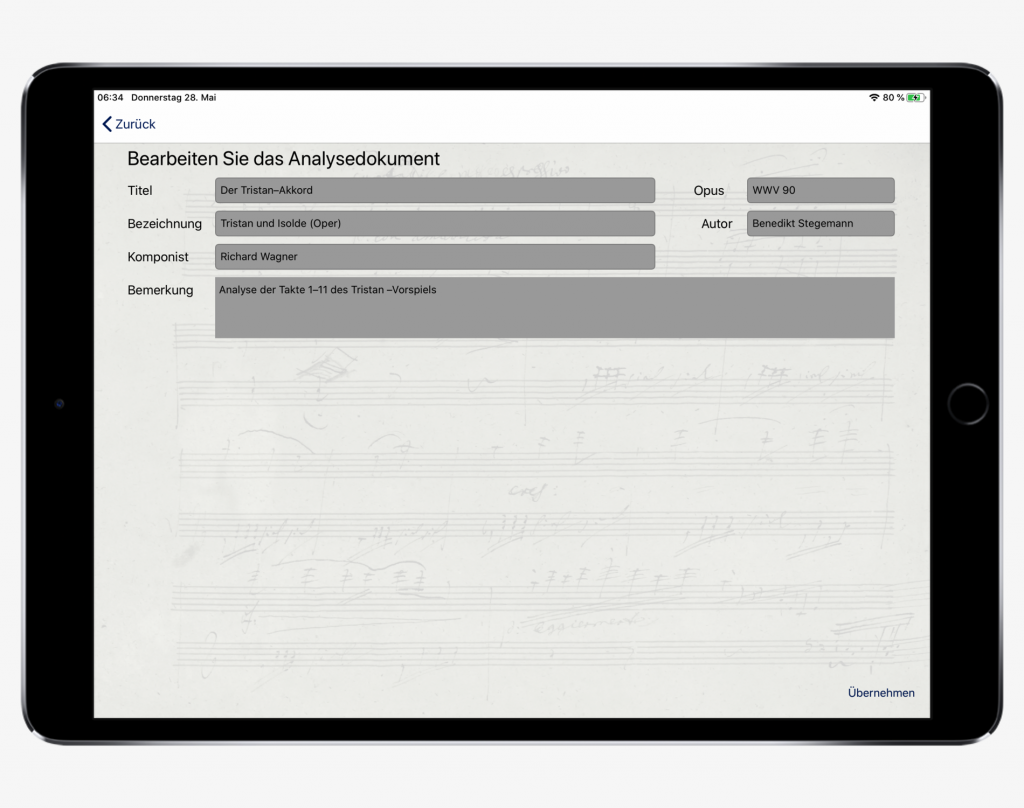
AEditing the completed metadata document

Functions of the input mask

After pressing theTristan-tile on the start page, the adjacent window opens. By touching the + symbol we are then forwarded to the input field. The following functions are available to us there:

By specifying bar and position, the chords are put in the correct order.
The intervals to be analyzed are entered using the virtual keyboard.
The black keys are divided into an area for the symbol # and one for the symbol b.
Chords with a minimum of two and a maximum of seven notes are analyzed. From the seven-tone onwards, all K-structures are always closed, which is why there is no need to enter additional tones.
The evaluation is initiated via the Analysis button. The ci existing in the chord are read out and assigned to their K-structures.
The Apply Apply (Übermehmen) button causes the result to be entered in a table. The interface is immediately available for entering the next chord.
The Undo(Rückgängig) removes the last tone entered.
The New (Neu) button removes all current entries even after an analysis has already been carried out. No transfer to the table takes place and the interface is free for a new input.

empty analysis table

empty input window

Analysis

We now analyze the chords of bars 1-11 of the Tristan prelude. Since the first chord is in bar 2, we first press the + symbol at bar (Takt) and then use the virtual keyboard to enter the tones f b d_# g_#of the first chord.

The app lists six intervals: three starting on the note f, two starting on the note b and one starting on the note d_#. Three of these intervals are ci; they are assigned to their respective K structure by the flags. The overall chord and an overview of the K structures excluded by the flags appear in the header. The content of the header line is transferred to a table after touching Apply (Übernehmen).

We now continue with the input of the chords and make sure that when a new bar is reached, the setting is adjusted via the input field. When we have analyzed all the chords in bars 1-11, the arrow button at the top left of the page takes us to the overview of the chords analyzed so far. If all entries were correct, it looks like the screenshot opposite. Apart from the initial sound, K V, the basis of the love key in E major, remains open.

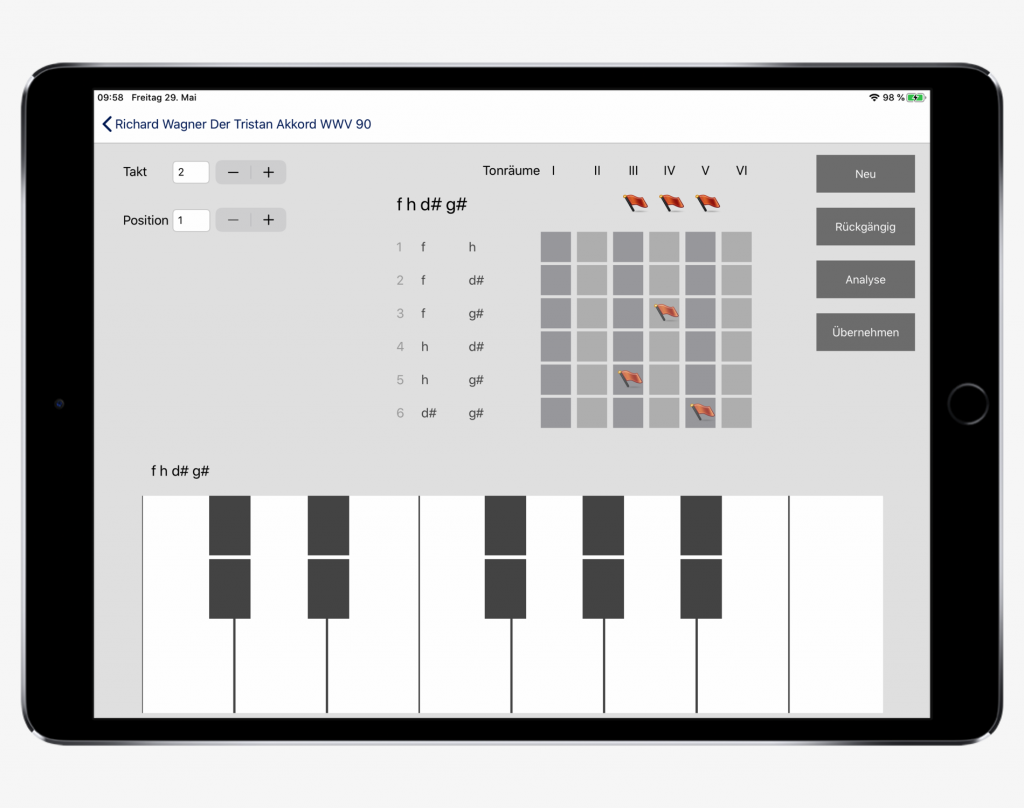
analyzed single chord with all analysis details

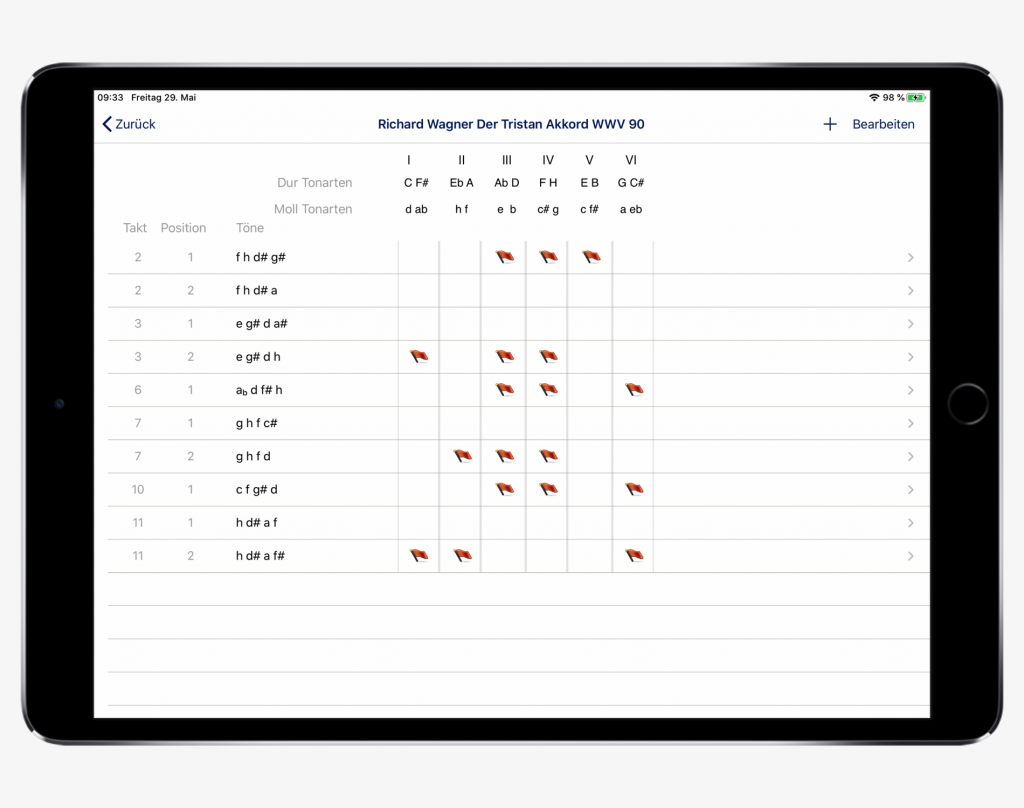
Overview of the analyzed chords

Edit and delete results

By tapping a line in the overview table, we are redirected to the input page and can make corrections. In this way, we can undo incorrect chord inputs or change the information about bar and position.

Swiping to the left activates the Delete a line (Löschen) button. By tapping Delete (Löschen) the chord is removed from the analysis.

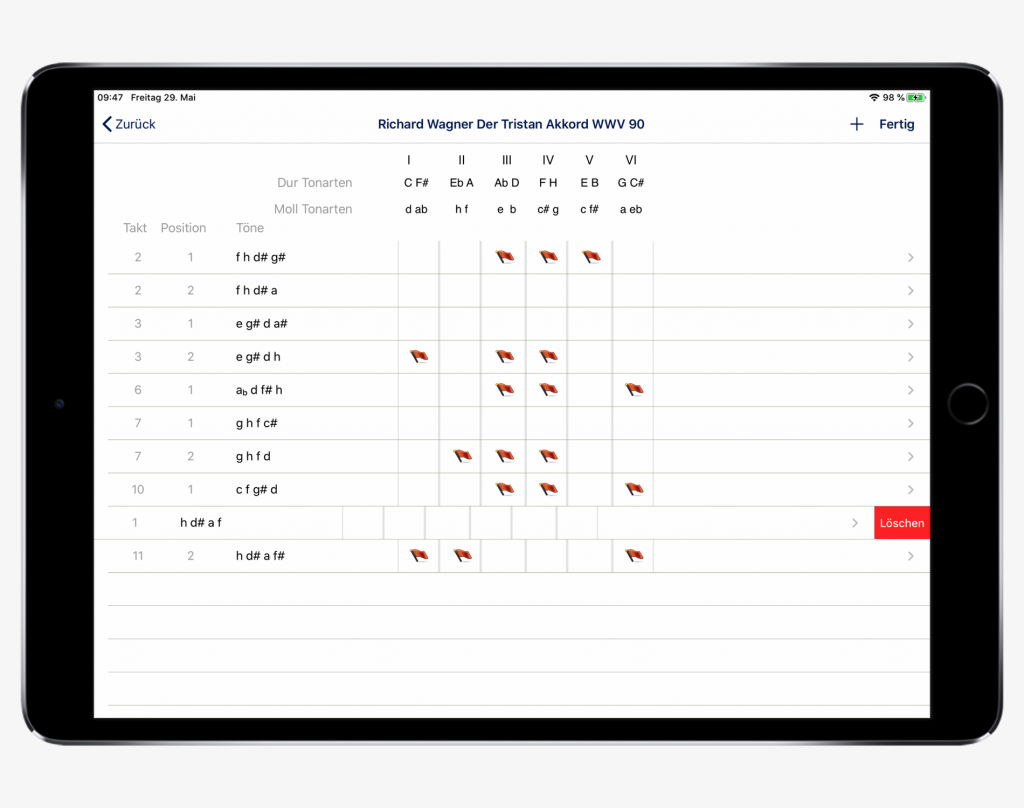
Deleting an analyzed chord

Export of the results

To export an analysis, we touch the corresponding field in the bar on the start page. We now have two options:

To send the complete file, we choose ciAnalysis document. By sending the complete file, it is possible to continue the analysis on another device. If the analysis is continued by another author, this author can be added to the metadata.
To send only the table with the analyzed intervals, we choose Table (Tabelle) . The table is shared as a CSV file and can be opened and processed by the recipient with programs like Excel or Numbers. This allows a fast processing of the data for a publication or presentation.

The exports can be sent directly from the iPad to an Airdrop-compatible device or they can be distributed via email.

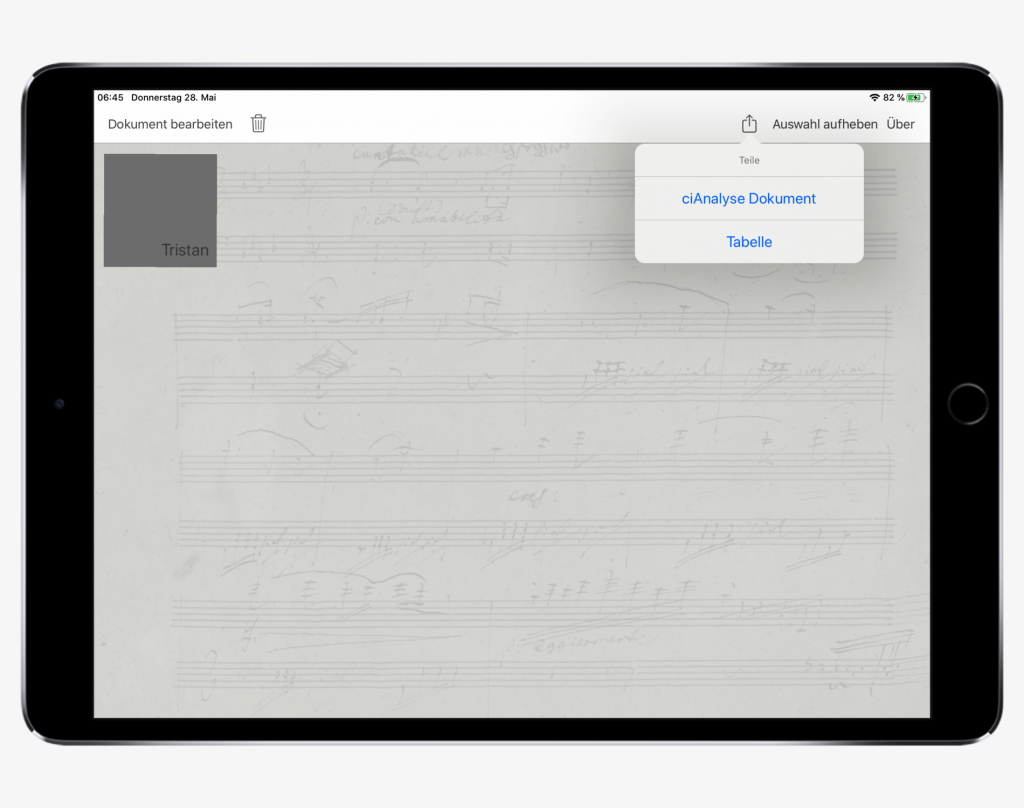
2 ways of exporting a cianalysis

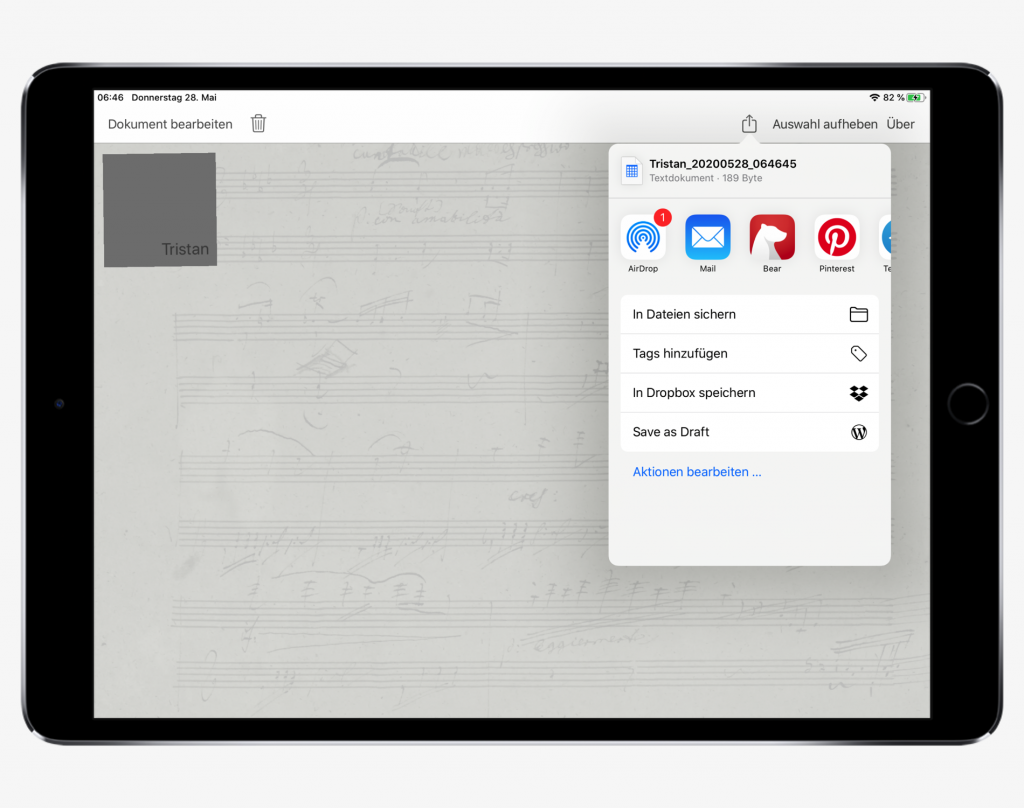
Exporting a cianalysis document

Export of the analysis table

Working with the analysis results

A table exported from the app can can also be processed e.g. with Numbers or Excel on the iPad without having to go via a desktop computer.

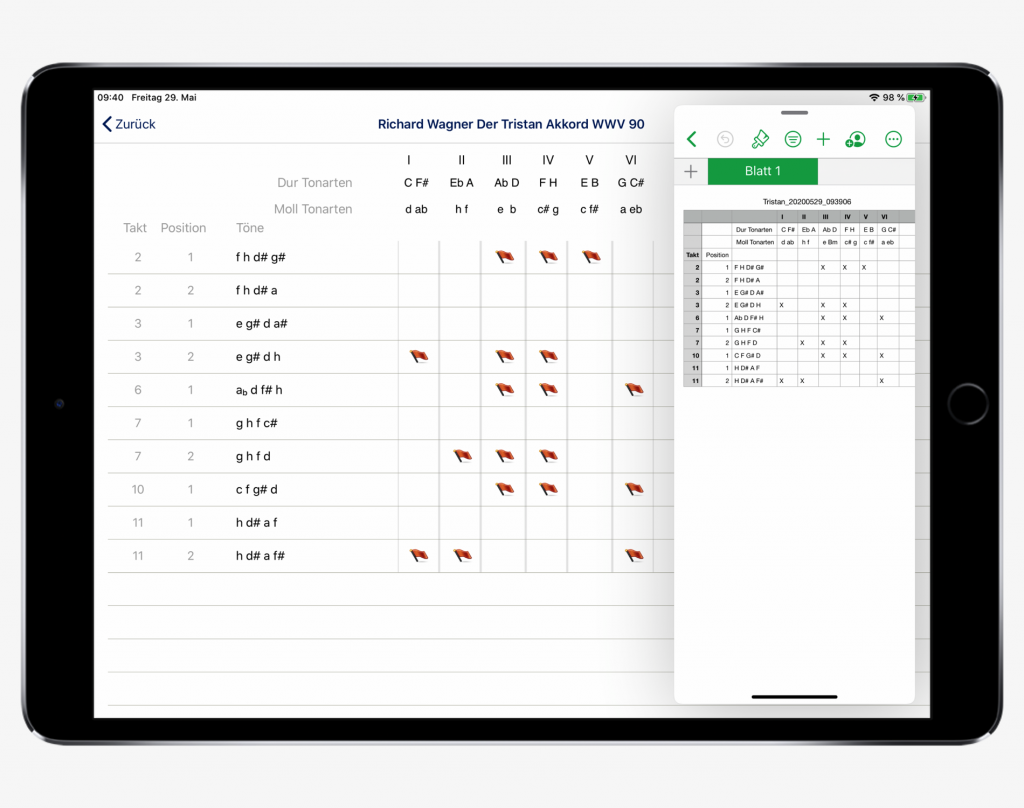
Further processing of an exported table